SPSS主成分分析与因子分析之比较及实证分析

一、问题的提出

在科学研究或日常生活中，常常需要判断某一事物在同类事物中的好坏、优劣程度及其发展规律等问题。而影响事物的特征及其发展规律的因素（指标）是多方面的，因此，在对该事物进行研究时，为了能更全面、准确地反映出它的特征及其发展规律，就不应仅从单个指标或单方面去评价它，而应考虑到与其有关的多方面的因素，即研究中需要引入更多的与该事物有关系的变量，来对其进行综合分析和评价。多变量大样本资料无疑能给研究人员或决策者提供很多有价值的信息，但在分析处理多变量问题时，由于众变量之间往往存在一定的相关性，使得观测数据所反映的信息存在重叠现象。因此为了尽量避 免信息重叠和减轻工作量，人们就往往希望能找出少数几个互不相关的综合变量来尽可能地反映原来数据所含有的绝大部分信息。而主成分分析和因子分析正是为解决此类问题而产生的多元统计分析方法。

近年来，这两种方法在社会经济问题研究中的应用越来越多，其应用范围也愈加广泛。因子分析是主成分分析的推广和发展，二者之间就势必有着许多共同之处，而 SPSS软件不能直接进行主成分分析，致使一些应用者在使用SPSS进行这两种方法的分析时，常常会出现一些混淆性的错误，这难免会使人们对分析结果产生质疑。因此，有必要在运用SPSS分析时，将这两种方法加以严格区分，并针对实际问题选择正确的方法。

二、主成分分析与因子分析的联系与区别

两种方法的出发点都是变量的相关系数矩阵，在损失较少信息的前提下，把多个变量（这些变量之间要求存在较强的相关性，以保证能从原始变量中提取主成分）综合成少数几个综合变量来研究总体各方面信息的多元统计方法，且这少数几个综合变量所代表的信息不能重叠，即变量间不相关。

主要区别：

1. 主成分分析是通过变量变换把注意力集中在具有较大变差的那些主成分上，而舍弃那些变差小的主成分；因子分析是因子模型把注意力集中在少数不可观测的潜在变量（即公共因子）上，而舍弃特殊因子。

2. 主成分分析是将主成分表示为原观测变量的线性组合，

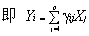 （1）

主成分的个数i=原变量的个数p，其中j=1,2,…,p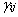， 是相关矩阵的特征值所对应的特征向量矩阵中的元素， 是原始变量的标准化数据，均值为0，方差为1。其实质是p维空间的坐标变换，不改变原始数据的结构。

而因子分析则是对原观测变量分解成公共因子和特殊因子两部分。因子模型如式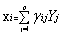（2），

 （2）

其中i=1,2,…,p, m

是因子分析过程中的初始因子载荷矩阵中的元素, 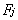是第j个公共因子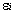，是第i个原观测变量的特殊因子。且此处的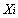与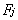的均值都为0，方差都为1。

3. 主成分的各系数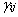，是唯一确定的、正交的。不可以对系数矩阵进行任何的旋转，且系数大小并不代表原变量与主成分的相关程度；而因子模型的系数矩阵是不唯一的、可以进行旋转的，且该矩阵表明了原变量和公共因子的相关程度。

4. 主成分分析，可以通过可观测的原变量X直接求得主成分Y，并具有可逆性；因子分析中的载荷矩阵是不可逆的，只能通过可观测的原变量去估计不可观测的公共因 子，即公共因子得分的估计值等于因子得分系数矩阵与原观测变量标准化后的矩阵相乘的结果。还有，主成分分析不可以像因子分析那样进行因子旋转处理。

5.综合排名。主成分分析一般依据第一主成分的得分排名，若第一主成分不能完全代替原始变量，则需要继续选择第二个主成分、第三个等等，此时综合得分=∑ （各主成分得分×各主成分所对应的方差贡献率）,主成分得分是将原始变量的标准化值，代入主成分表达式中计算得到；而因子分析的综合得分=∑（各因子得分 ×各因子所对应的方差贡献率）÷∑各因子的方差贡献率，因子得分是将原始变量的标准化值，代入因子得分函数中计算得到。

区别中存联系，联系中显区别

由于上文提到主成分可表示为原观测变量的线性组合，其系数为原始变量相关矩阵的特征值所对应的特征向量，且这些特征向量正交，因此，从X到Y的转换关系是可逆的，便得到如下的关系：

 　 （3）

下面对其只保留前m个主成分（贡献大），舍弃剩下贡献很小的主成分，得：

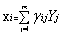　　　　i=1,2,…p　　　　　（4）

由此可见，式（4）在形式上已经与因子模型（2）忽略特殊因子后的模型即：

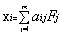 （2）*

相一致，且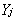 （j=1,2,…,m）之间相互独立。由于模型（2）*是因子分析中未进行因子载荷旋转时建立的模型，故如果不进行因子载荷旋转，许多应用者将容易把此时的因子分析理解成主成分分析，这显然是不正确的。

然而此时的主成分的系数阵即特征向量与因子载荷矩阵确实存在如下关系：

主成分分析中，主成分的方差等于原始数据相关矩阵的特征根，其标准差也即特征根的平方根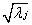，于是可以将除以其标准差（单位化）后转化成合适的公因子，即令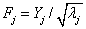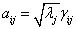，，则式（4）变为：

 （4）*

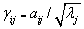可得，　 （5）

式（5）便是主成分系数矩阵与初始因子载荷阵之间的联系。不能简单地将初始因子载荷矩阵认为是主成分系数矩阵（特征向量矩阵），否则会造成偏差。

三、实证分析

通过实例来研究SPSS软件中的因子分析和主成分分析及二者分析结果的比较。运用两种分析方法对2005年江苏省13个主要城市的经济发展综合水平进行分析。

本文在选取指标时遵循了指标选取的基本原则，即针对性、可操作性、层次性、全面性等原则，选取了以下反映城市经济发展综合水平的9项指标： GDP(X1)亿元 、人均GDP (X2) 元 、城镇居民人均可支配收入(X3)元、农村居民纯收入(X4) 元、第三产业占GDP比重(X5)%、金融机构存款余额（X6）亿元、万人中各专业技术人员数(X7)人、科技三项和文教科卫支出（X8）亿元、实际利用 外资(X9) 亿美元。

（一） 数据来源及处理

按照上述指标体系，选取了江苏13个城市的数据，（所有数据均来源于《江苏统计年鉴（2006）》）。指标都是正指标，无需归一化，SPSS13.0将自动对原始数据进行标准差标准化处理，消除指标量纲及数量级的影响。

（二） 运用SPSS进行分析

首先，通过SPSS中的Data Reduction-Factor命令进行因子分析，本文采取主成分分析法来抽取公共因子，并依据特征值大于1来确定因子数目。

相关的分析结果及分析，如下：

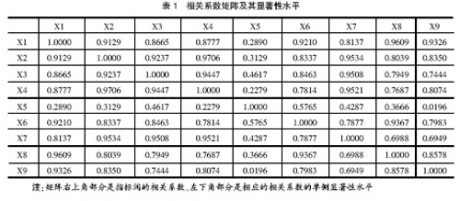
1.相关系数矩阵

由于因子分析是基于相关矩阵进行的，即要求各指标之间具有一定的相关性，求出相关矩阵是必要的。KMO统计量是0.659，且Bartlett球体检验 值为190.584，卡方统计值的显著性水平为0.000小于0.01，都说明各指标之间具有较高相关性，因此本文数据适用于作因子分析。

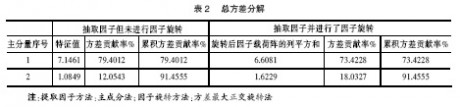
2.总方差分解

表2中，依据特征值大于1的原则，提取了2个公因子（主成分），它们的累积方差贡献率达91.4555%，这2个公因子（主成分）包含了原指标的绝大部分信息，可以代替原来9个变量对城市经济发展水平现状进行衡量。

3.主成分表达式与因子模型

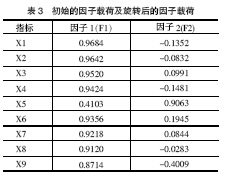
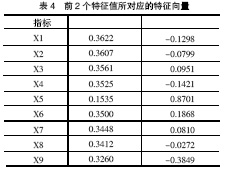
初始因子载荷矩阵（见表3）反映了公因子与原始变量之间的相关程度，而主成分的系数矩阵并不反映公因子与原始变量之间的相关程度，故不能直接用表3中的 数据表示。根据该系数矩阵与初始因子载荷阵之间的关系（如式（5）），可以计算出前2个特征值所对应的特征向量阵（系数矩阵），见表4。

很明显表4和表3中的数据相差很大，因此，如果将初始因子载荷阵误认为是主成分系数矩阵，分析结果将会产生较大偏差。

主成分的表达式应为：（6）
Y1=0.3622 *Z1+0.3607 *Z2+…+0.3260*Z9
Y2=-0.1298 *Z1-0.0799 *Z2+…-0.3849*Z9
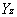=（79.4012* Y1+12.0543* Y2）/100

因子模型：
X1=0.9684*F1-0.1352*F2
X2=0.9642*F1-0.0832*F2
…
X9=0.8714*F1-0.4009*F2
其中Z1~Z9是X1~X9的标准化数据.

4.因子得分函数

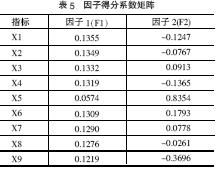
从表3得知，各因子在各变量上的载荷已经向0和1两极分化，故无需进行因子旋转。公因子是不可观测的，估计因子得分应借助于未旋转因子得分系数矩阵，见表5。

得到以下因子得分函数：（7）
F1=0.1355*Z1+0.1349*Z2 +…+0.1219*Z9
F2=-0.1247 *Z1-0.0767*Z2 +…-0.3696*Z9
同样Z1~Z9是标准化的数据，其综合得分计算公式：
=(73.4228*F1+18.0327*F2)/91.4555（8）

（三） 两种方法综合排名比较

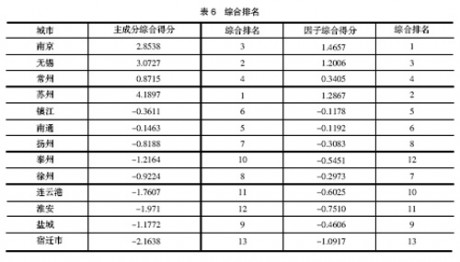
按照主成分综合得分和因子综合得分，对江苏13个城市的经济发展综合水平进行排名，见表6。

表6中，综合得分出现负值，这只表明该城市的综合水平处于平均水平之下（由于主成分（因子）已经标准化了）。

从该表看出，主成分分析与因子分析的实证结果，不仅大部分城市的排名存在差异，且综合得分值上存在较大差异，其定量值差异较大，这对于后来的综合定量定性分析，最终所提出的政策建议等都会产生较大影响。因此不能混用。

四、结束语

使用主成分分析和因子分析进行综合评价时，可以通过不同的统计软件来完成数据分析，除SPSS软件外，其他软件都分别设有两种方法的过程命令，使用者可以根据需要采用其中一种来分析问题，一般不会混淆。而正是因为SPSS没有直接进行主成分分析的命令，才使得那些本身尚未清楚区分这两种方法的使用者更加迷惑，不慎便会出现混淆性错误。因此，本文很详细地从理论和实证角度，分析了这两种方法的异同及如何运用SPSS软件进行分析。从实证结果看，运用主成分分析和因子分析进行综合定量分析时，不但综合排名结果存在差异，而且定量值也存在较大差异，这必然会影响后面的综合定性分析结果。因此，我们应正确理解和运用这两种方法，使其发挥出各自最大的优势，以便更好地服务于实际问题的分析。