 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
朴素贝叶斯分类和预测算法的原理及实现
决策树和朴素贝叶斯是最常用的两种分类算法,本篇文章介绍朴素贝叶斯算法。贝叶斯定理是以英国数学家贝叶斯命名,用来解决两个条件概率之间的关系问题。简单的说就是在已知P(A|B)时如何获得P(B|A)的概率。朴素贝叶斯(Naive Bayes)假设特征P(A)在特定结果P(B)下是独立的。
在开始介绍贝叶斯之前,先简单介绍下概率的基础知识。概率是某一结果出现的可能性。例如,抛一枚匀质硬币,正面向上的可能性多大?概率值是一个0-1之间的数字,用来衡量一个事件发生可能性的大小。概率值越接近1,事件发生的可能性越大,概率值越接近0,事件越不可能发生。我们日常生活中听到最多的是天气预报中的降水概率。概率的表示方法叫维恩图。下面我们通过维恩图来说明贝叶斯公式中常见的几个概率。
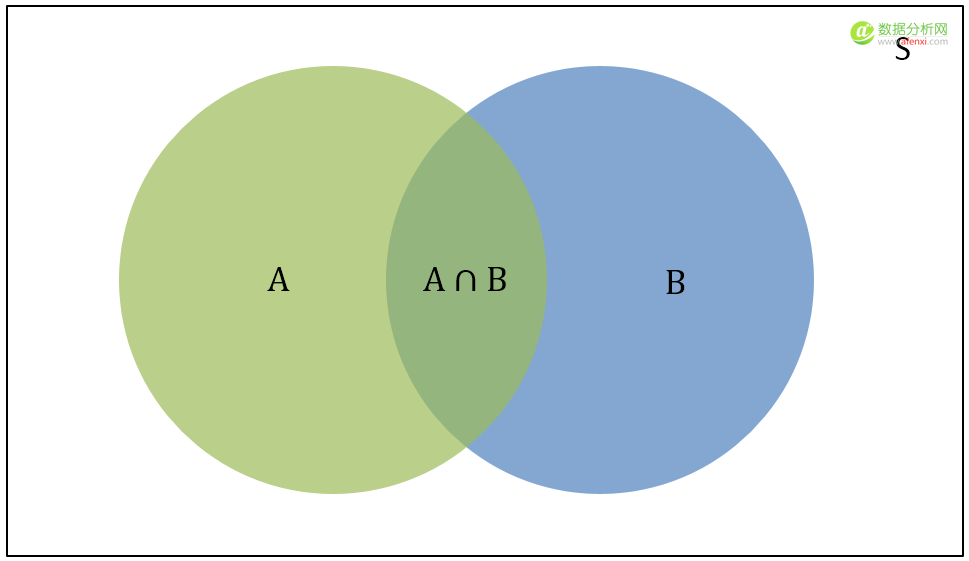
在维恩图中:
S:S是样本空间,是所有可能事件的总和。
P(A):是样本空间S中A事件发生的概率,维恩图中绿色的部分。
P(B):是样本空间S中B事件发生的概率,维恩图中蓝色的部分。
P(A∩B):是样本空间S中A事件和B事件同时发生的概率,也就是A和B相交的区域。
P(A|B):是条件概率,是B事件已经发生时A事件发生的概率。
对于条件概率,还有一种更清晰的表示方式叫概率树。下面的概率树表示了条件概率P(A|B)。与维恩图中的P(A∩B)相比,可以发现两者明显的区别。P(A∩B)是事件A和事件B同时发现的情况,因此是两者相交区域的概率。而事件概率P(A|B)是事件B发生时事件A发生的概率。这里有一个先决条件就是P(B)要首先发生。

因为条件概率P(A|B)是在事件B已经发生的情况下,事件A发生的概率,因此P(A|B)可以表示为事件A与B的交集与事件B的比率。
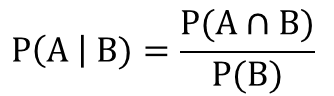
该公式还可以转换为以下形式,以便我们下面进行贝叶斯公式计算时使用。
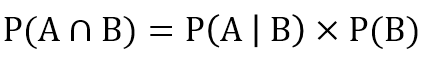
贝叶斯算法通过已知的P(A|B),P(A),和P(B)三个概率计算P(B|A)发生的概率。假设我们现在已知P(A|B),P(A)和P(B)三个概率,如何计算P(B|A)呢?通过前面的概率树及P(A|B)的概率可知,P(B|A)的概率是在事件A发生的前提下事件B发生的概率,因此P(B|A)可以表示为事件B与事件A的交集与事件A的比率。
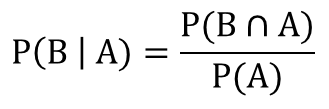
该公式同样可以转化为以下形式:
![]()
到这一步,我们只需要证明P(A∩B)= P(B∩A)就可以证明在已知P(A|B)的情况下可以通过计算获得P(B|A)的概率。我们将概率树转化为下面的概率表,分别列出P(A|B),P(B|A),P(A),和P(B)的概率。
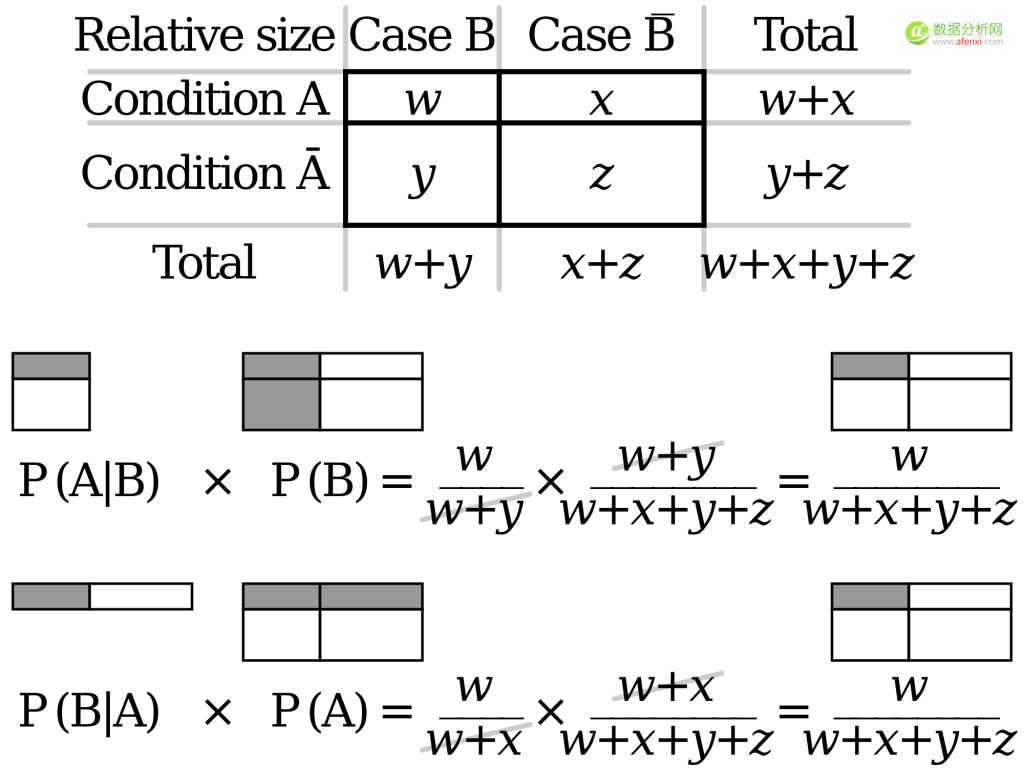
通过计算可以证明P(A|B)*P(B)和P(B|A)*P(A)最后求得的结果是概率表中的同一个区域的值,因此:

我们通过P(A∩B)= P(B∩A)证明了在已知P(A|B),P(A),和P(B)三个概率的情况下可以计算出P(B|A)发生的概率。整个推导和计算过程可以说得通。但从统计学的角度来看,P(A|B)和P(B|A)两个条件概率之间存在怎样的关系呢?我们从贝叶斯推断里可以找到答案。
贝叶斯推断可以说明贝叶斯定理中两个条件概率之间的关系。换句话说就是我们为什么可以通过P(A|B),P(A),和P(B)三个概率计算出P(B|A)发生的概率。

在贝叶斯推断中,每一种概率都有一个特定的名字:
P(B)是”先验概率”(Prior probability)。
P(A)是”先验概率”(Prior probability),也作标准化常量(normalized constant)。
P(A|B)是已知B发生后A的条件概率,叫做似然函数(likelihood)。
P(B|A)是已知A发生后B的条件概率,是我们要求的值,叫做后验概率。
P(A|B)/P(A)是调整因子,也被称作标准似然度(standardised likelihood)。
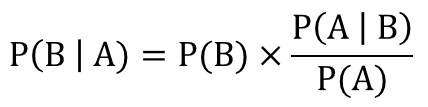
贝叶斯推断中有几个关键的概念需要说明下:
第一个是先验概率,先验概率是指我们主观通过事件发生次数对概率的判断。
第二个是似然函数,似然函数是对某件事发生可能性的判断,与条件概率正好相反。通过事件已经发生的概率推算事件可能性的概率。
维基百科中对似然函数与概率的解释:
概率:是给定某一参数值,求某一结果的可能性。
例如,抛一枚匀质硬币,抛10次,6次正面向上的可能性多大?
似然函数:给定某一结果,求某一参数值的可能性。
例如,抛一枚硬币,抛10次,结果是6次正面向上,其是匀质的可能性多大?
第三个是调整因子:调整因子是似然函数与先验概率的比值,这个比值相当于一个权重,用来调整后验概率的值,使后验概率更接近真实概率。调整因子有三种情况,大于1,等于1和小于1。
因此,贝叶斯推断可以理解为通过先验概率和调整因子来获得后验概率。其中调整因子是根据事件已经发生的概率推断事件可能发生的概率(通过硬币正面出现的次数来推断硬币均匀的可能性),并与已经发生的先验概率(硬币正面出现的概率)的比值。通过这个比值调整先验概率来获得后验概率。
后验概率 = 先验概率 x 调整因子
贝叶斯分类器比较有名的实验场景是对垃圾邮件进行分类和过滤。这里我们简单介绍下通过贝叶斯算法过滤垃圾邮件的过程。贝叶斯分类器需要依赖历史数据进行学习,假定包含关键词”中奖”的就算作垃圾邮件。我们先经过人工筛选找出10封邮件,并对包含关键词”中奖“的邮件标注为垃圾邮件(Spam)。

我们将普通邮件和垃圾邮件中出现“中奖”关键词的频率进行汇总,分别记录普通邮件中出现和未出现该关键词的次数和垃圾邮件中出现和未出现该关键词的次数,并分别进行汇总。
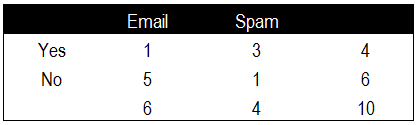
根据频率表计算出贝叶斯算法中所需的关键概率值,这里我们已知普通邮件的概率P(Email),垃圾邮件的概率P(Spam),出现关键词的概率P(Yes),未出现关键词的概率P(No),以及垃圾邮件出现关键词的概率P(Yes|Spam)。

按照贝叶斯公式,已知P(B|A),P(A)和P(B)的概率。求P(A|B)的概率。

我们将贝叶斯公式套用到垃圾邮件分类中,已知垃圾邮件中出现“中奖”关键词的概率,和垃圾邮件及“中奖”关键词的概率,求出现“中奖”关键词是垃圾邮件的概率。
P(A)=P(垃圾邮件)=0.40
P(B)=P(出现关键词)=0.40
P(B|A)=P(出现关键词|垃圾邮件)=0.75
P(A|B)=P(垃圾邮件|出现关键词)

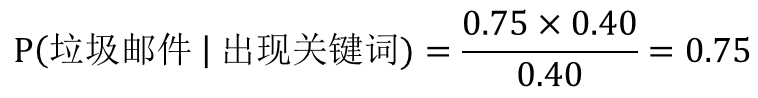
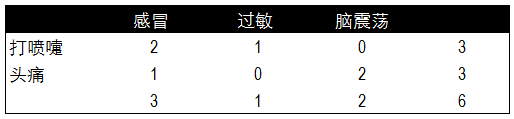
除了垃圾邮件分类,再来看一个病情预测的实例。通过历史数据已知几类疾病的病症及 患病人职业。那么如果新来的一位打喷嚏的建筑工人,如何通过贝叶斯算法通过历史数据来预测这位打喷嚏的建筑工人患感冒的概率呢?以下是6位历史病例的数据。

根据疾病的种类,我们分别对不同病症和不同职业患病的频率进行了统计。以下分别是不同症状与对应疾病发生的频率表,和不同职业与所对应疾病发生的频率表。
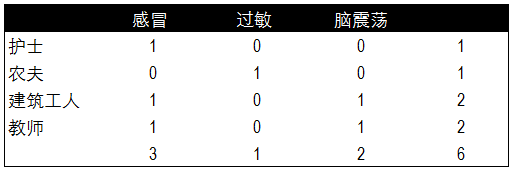
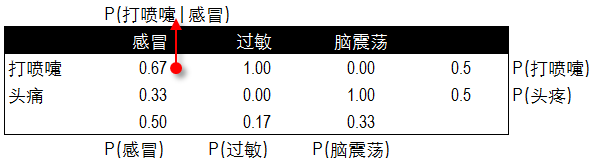
根据两个频率表分布计算出贝叶斯算法中所需的概率值,这里我们已知每种疾病的概率,不同职业和不同症状的概率,以及患感冒后打喷嚏和职业为建筑工人的概率。

按照贝叶斯公式,已知P(B*C|A),P(A)和P(B*C)的概率。求P(A|B*C)的概率。
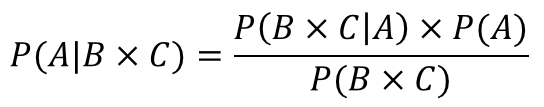
我们假设护士和打喷嚏这两个特征在感冒这个结果下是独立的,因此,上面的贝叶斯公式可以转化为朴素贝叶斯公式:
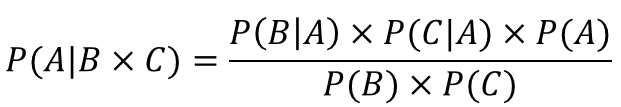
我们将贝叶斯公式套用到疾病预测中:
P(A)=P(感冒)=0.5
P(B)=P(打喷嚏)=0.5
P(C)=P(建筑工人)=0.33
P(B|A)= P(打喷嚏|感冒)=0.67
P(C|A)= P(建筑工人|感冒)=0.33

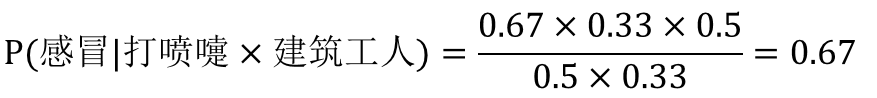

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
B+树作为数据库索引的核心数据结构,其高效的查询、插入、删除性能,离不开节点间指针的合理设计。在日常学习和数据库开发中,很 ...
2026-01-30在数据库开发中,UUID(通用唯一识别码)是生成唯一主键、唯一标识的常用方式,其标准格式包含4个短横线(如550e8400-e29b-41d4- ...
2026-01-30商业数据分析的价值落地,离不开标准化、系统化的总体流程作为支撑;而CDA(Certified Data Analyst)数据分析师,作为经过系统 ...
2026-01-30在数据分析、质量控制、科研实验等场景中,数据波动性(离散程度)的精准衡量是判断数据可靠性、稳定性的核心环节。标准差(Stan ...
2026-01-29在数据分析、质量检测、科研实验等领域,判断数据间是否存在本质差异是核心需求,而t检验、F检验是实现这一目标的经典统计方法。 ...
2026-01-29统计制图(数据可视化)是数据分析的核心呈现载体,它将抽象的数据转化为直观的图表、图形,让数据规律、业务差异与潜在问题一目 ...
2026-01-29箱线图(Box Plot)作为数据分布可视化的核心工具,能清晰呈现数据的中位数、四分位数、异常值等关键统计特征,广泛应用于数据分 ...
2026-01-28在回归分析、机器学习建模等数据分析场景中,多重共线性是高频数据问题——当多个自变量间存在较强的线性关联时,会导致模型系数 ...
2026-01-28数据分析的价值落地,离不开科学方法的支撑。六种核心分析方法——描述性分析、诊断性分析、预测性分析、规范性分析、对比分析、 ...
2026-01-28在机器学习与数据分析领域,特征是连接数据与模型的核心载体,而特征重要性分析则是挖掘数据价值、优化模型性能、赋能业务决策的 ...
2026-01-27关联分析是数据挖掘领域中挖掘数据间潜在关联关系的经典方法,广泛应用于零售购物篮分析、电商推荐、用户行为路径挖掘等场景。而 ...
2026-01-27数据分析的基础范式,是支撑数据工作从“零散操作”走向“标准化落地”的核心方法论框架,它定义了数据分析的核心逻辑、流程与目 ...
2026-01-27在数据分析、后端开发、业务运维等工作中,SQL语句是操作数据库的核心工具。面对复杂的表结构、多表关联逻辑及灵活的查询需求, ...
2026-01-26支持向量机(SVM)作为机器学习中经典的分类算法,凭借其在小样本、高维数据场景下的优异泛化能力,被广泛应用于图像识别、文本 ...
2026-01-26在数字化浪潮下,数据分析已成为企业决策的核心支撑,而CDA数据分析师作为标准化、专业化的数据人才代表,正逐步成为连接数据资 ...
2026-01-26数据分析的核心价值在于用数据驱动决策,而指标作为数据的“载体”,其选取的合理性直接决定分析结果的有效性。选对指标能精准定 ...
2026-01-23在MySQL查询编写中,我们习惯按“SELECT → FROM → WHERE → ORDER BY”的语法顺序组织语句,直觉上认为代码顺序即执行顺序。但 ...
2026-01-23数字化转型已从企业“可选项”升级为“必答题”,其核心本质是通过数据驱动业务重构、流程优化与模式创新,实现从传统运营向智能 ...
2026-01-23CDA持证人已遍布在世界范围各行各业,包括世界500强企业、顶尖科技独角兽、大型金融机构、国企事业单位、国家行政机关等等,“CDA数据分析师”人才队伍遵守着CDA职业道德准则,发挥着专业技能,已成为支撑科技发展的核心力量。 ...
2026-01-22在数字化时代,企业积累的海量数据如同散落的珍珠,而数据模型就是串联这些珍珠的线——它并非简单的数据集合,而是对现实业务场 ...
2026-01-22