作者丨algorithmia

来源 | 大数据与人工智能

机器学习中的线性回归是一种来源于经典统计学的有监督学习技术。然而，随着机器学习和深度学习的迅速兴起，因为线性（多层感知器）层的神经网络执行回归，线性回归的使用也日益激增。

这种回归通常是线性的，但是当把非线性激活函数合并到这些网络中时，它们就可以执行非线性回归。

非线性回归使用某种形式的非线性函数（例如多项式或指数）对输入和输出之间的关系进行建模。非线性回归可以用来模拟科学和经济学中常见的关系，例如，放射性分子的指数衰减或股票市场的走势与全球经济的整体走势一致。

线性回归如何工作？

从神经网络的观点来看，我们可以将线性回归模型指定为一个简单的数学关系。简单来说，线性回归是在输入变量和输出变量之间建立一个线性依赖关系模型。根据所处的工作环境，这些输入和输出使用不同的术语来引用。

最常见的是一个包含k个示例的训练数据集，每个示例都有n个输入分量

称为回归变量、协变量或外生变量。输出向量y称为响应变量、输出变量或因变量。在多元线性回归中，可以有多个这样的输出变量。模型的参数

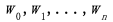
被称为回归系数，或者在深度学习环境中称为权重。对于单个训练示例

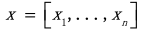
，该模型具有以下形式：

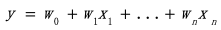
我们还可以通过将训练数据压缩到矩阵中：

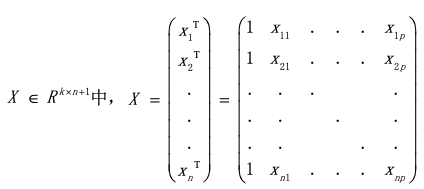
以此将权重压缩到矢量

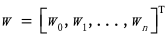
中来简化这种表示法。权重构成了模型的核心。它们对输入和输出之间的线性关系进行编码，从而更加重视重要的数据特征，并降低不重要的数据特征的权重。注意，我们向X值为1的每一行添加了一个“隐藏组件”。这让我们能够计算w的点积，其偏置项为

。偏置项允许模型将其计算的线性超平面移开原点，从而允许模型对非零中心数据中的关系进行建模。简化后的模型可以表示为

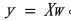
这是大多数线性回归实现的基础模型。然而，在此基本结构上可以存在许多变体，每种变体都有其自身的缺点和益处。例如，有一个线性回归版本称为贝叶斯线性回归，它通过在模型的权重上放置先验分布来引入一个贝叶斯观点。这样可以更容易地推断模型正在做什么，随后使其结果更具有解释性。

训练线性回归模型

那么我们如何训练线性回归模型呢？这个过程类似于大多数机器学习模型所使用的过程。假设我们有一套训练集

，任务是在不影响模型对新示例预测能力的情况下，尽可能紧密地对这种关系进行建模。为此，我们定义一个损失或目标函数

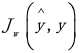
输入真实输出y和预测输出

，并测量了给定x时模型在预测y时的“好坏程度”。我们使用下标w来表示J的输出取决于模型的权重w，并通过预测y对其进行参数化，即使这些权重值未明确显示在函数的计算中。线性回归通常使用均方误差（MSE）损失函数，定义为：

然后，我们可以使用多种技术之一来优化此损失函数。我们可以使用例如梯度下降法，它是训练神经网络的实际标准，但是对于线性回归来说不是必要的。因为我们其实可以直接解决优化问题，以便找到权重的最佳值w*。

由于我们想要针对w优化此设置，对w取梯度，将结果设置为0，然后求解w的最优设置w*。我们有

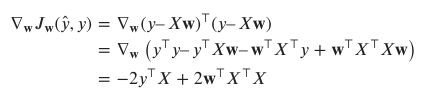
现在我们将梯度设置为0并求解w

这是w的最优设置，将为模型提供最佳结果。你可以看到，它仅使用X和y的乘积来计算。然而，它需要

的矩阵求逆，当X非常大或条件不佳时，这在计算上会很困难。在这些情况下，你可以使用不精确的优化方法如梯度下降法或不实际计算矩阵逆的近似技术。

正则化

线性回归最常用的变形可能是那些涉及加法正则化的模型。正则化是指对绝对值较大的模型权重进行惩罚的过程。通常这是通过计算一些权重的范数作为附加在成本函数上的惩罚项来完成的。

正则化的目的通常是为了减轻过度拟合的可能性，过度拟合是模型过于紧密地复制其训练数据中基础关系的趋势，无法将其很好地推广到未知示例中。线性回归模型的正则化有两种基本类型：L1和L2。

采用L1正则化的回归模型可以执行Lasso回归。L1规范定义为：

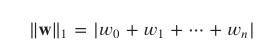
相反，L2正则化将权重向量w的L2范数作为惩罚项添加到目标函数中。 L2规范定义为：

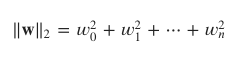
采用L2正则化的回归模型被称为执行Ridge回归（岭回归）。

那么，这些正则化惩罚如何定性地影响模型的结果（输出）的呢？结果表明，L2正则化产生的权重系数很小，但很分散。也就是说，它倾向于生成其中每个系数

相对较小并且幅度相对相似的模型。

相比之下，L1正则化在惩罚系数的方式上更加具体。其中某些系数往往受到严重的惩罚，趋向于0的值，而有些则保持相对不变。L1正则化产生的权值通常被认为是稀疏的。

因此，也有人认为，L1正则化实际上执行了一种软特征选择，即选择对产生期望结果最重要的特征（数据中的分量）。通过将某些权重设为0，该模型表明这些变量实际上对其作用并没有特别的帮助或解释作用。

线性回归的应用

线性回归可以用在数据中任何可能存在线性关系的地方。对于企业来说，这可能会以销售数据的形式出现。例如，一家企业可能向市场推出一种新产品，但不确定在什么价格销售。

通过在几个选定的价格点上以总销售额的形式测试客户的响应，企业可以使用线性回归推断价格和销售额之间的关系，从而确定销售产品的最佳点。

同样，线性回归可以应用在产品采购和生产线的许多阶段。例如，一个农民可能想要模拟某些环境条件（例如降雨和湿度）的变化如何影响总体农作物产量。这可以帮助他确定一个优化的系统，用于种植和轮作农作物，以实现利润最大化。

最后，线性回归是对数据中简单关系建模的宝贵工具。虽然它不像更现代的机器学习方法那么花哨或复杂，但它通常是许多存在直接关系的现实世界数据集的正确工具。更不用说，建立回归模型的简单性和对它们进行训练的快速性，使其成为那些想要快速有效地进行建立模型的企业的首选工具。