当我们只有非常少量的已标记数据，同时有大量未标记数据点时，可以使用半监督学习算法来处理。在sklearn中，基于图算法的半监督学习有Label Propagation和Label Spreading两种。他们的主要区别是第二种方法带有正则化机制。

我们在上篇已经讲解了Label Propagation，本篇我们讲解带有正则的Label Spreading。首先生成一些凹的数据。

# 生成环形数据
import numpy as np
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=200, shuffle=False)
outer, inner = 0, 1
labels = np.full(200, -1.0)
labels[0] = outer
labels[-1] = inner

# 画图
import matplotlib.pyplot as plt
plt.figure(figsize=(4, 4))
plt.scatter(X[labels == outer, 0], X[labels == outer, 1],)
plt.scatter(X[labels == inner, 0], X[labels == inner, 1],)
plt.scatter(X[labels == -1, 0], X[labels == -1, 1], marker=".",);

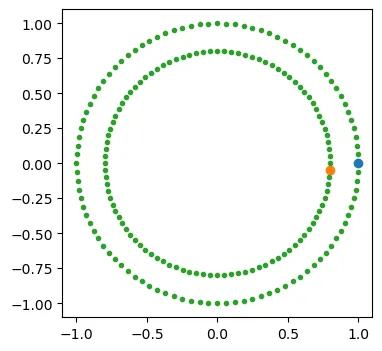
Label Spreading（标签扩散）算法是一种用于半监督学习的方法，它在Label Propagation的基础上引入了正则化机制。这种机制使得算法在处理噪声数据时更为稳定和健壮。下面是Label Spreading算法的迭代计算过程的详细介绍：

1、构建图

和Label Propagation一样，Label Spreading首先构建一个图，图中的每个节点代表一个数据样本，节点可以是已标记的也可以是未标记的。

2、计算相似性权重

节点之间的边表示数据点之间的相似性。这种相似性通常用距离度量（如欧氏距离）或核函数（如高斯核）来计算。边的权重反映了两个数据点之间的相似度。

3、初始化标签信息

每个数据点都有一个标签分布向量。对于已标记的数据，这个向量直接表示其标签信息。对于未标记的数据，初始时这个向量通常是均匀分布，或者有其他的初始化方法。

4、构建传播矩阵

Label Spreading算法构建了一个传播矩阵，用于在迭代过程中更新标签信息。这个矩阵基于节点的相似性权重，但与Label Propagation不同的是，它会引入一个正则化项。

5、迭代更新标签

在每次迭代中，对于每个未标记节点，其标签分布根据邻居节点（包括已标记和未标记的节点）的标签信息进行更新。具体地，一个节点的新标签分布是其所有邻居节点的标签分布的加权平均，这个权重由传播矩阵给出。

6、应用正则化

正则化是Label Spreading的一个关键特点。它帮助算法抵抗噪声和过拟合，提高了算法的鲁棒性。正则化参数控制着标签信息在未标记数据之间传播的强度。

7、归一化标签分布

更新完所有未标记节点的标签分布后，这些分布通常需要被归一化，确保它们是有效的概率分布。

8、收敛判断

算法重复迭代更新过程，直到满足某个收敛条件，如迭代次数上限或者标签分布的变化小于某个阈值。

9、确定最终标签

一旦算法收敛，每个未标记数据点的标签被确定为其标签分布中概率最高的标签。

关键要点

• 正则化机制：正则化帮助算法在处理噪声数据和不完全标记的数据时保持稳定。
• 适用性：Label Spreading适用于有大量未标记数据的情况，尤其当数据包含噪声或者不完全标记时。
• 灵活性与稳健性：算法的性能依赖于图的构建方式、相似性度量的选择，以及正则化参数的设定。

总的来说，Label Spreading是一个强大而灵活的工具，适用于各种半监督学习场景，尤其是在数据标签稀缺或包含噪声的情况下。

在实际应用中，银行利用标签处理技术构建反欺诈模型，通过对用户行为、交易特征等多维度数据进行分析，定义并应用各种风险标签。这些标签可以帮助银行快速识别异常交易行为，提升反欺诈能力。例如，通过分析黑样本案例特征，银行可以定义如“当天还款后立即交易”等标签，并将其应用于反诈模型的开发和训练。

在Label Spreading算法中，正则化传播矩阵是核心组件之一，用于在迭代过程中调整和传播标签信息。这个传播矩阵通过结合图的相似性结构和正则化机制，有效地平衡了标签信息的传播和抗噪声能力。以下是正则化传播矩阵的关键点：

1、构建图和相似性矩阵

首先，算法构建一个图，为每个数据点准备一个标签矩阵Y。对于已标记的数据点，标签矩阵的相应行用其标签的独热编码（one-hot encoding）表示；对于未标记的数据点，标签矩阵的相应行初始化为均匀分布或其他方式。

然后，基于KNN或RBF核等方法计算相似性矩阵（通常表示为S），其中每个元素Sij表示节点i和j之间的相似度。

2、归一化相似性矩阵

相似性矩阵接着被归一化，以便每个节点的相似度总和为1。这可以通过对矩阵S 的每一行进行归一化来实现，得到归一化的矩阵T。

3、正则化传播矩阵

正则化传播矩阵由归一化的相似性矩阵和一个正则化参数α构建而成。通常，P的计算公式为

其中I是单位矩阵，α是一个介于0和1之间的参数，用于控制传播过程中的正则化程度。

4、正则化参数α

作用：参数α控制了标签信息在原始标签和邻居标签间的平衡。较小的α值更强调邻居节点的标签信息，而较大的α值使算法更加倾向于保持原始标签。 抗噪声能力：通过调整α，Label Spreading算法能够在保持数据内在结构的同时对噪声数据具有一定的抵抗力。

5、标签更新和传播

在每次迭代中，当前的标签矩阵Y通过乘以传播矩阵P来更新，即

这样，每个数据点的新标签不仅反映了其邻居的标签信息，也考虑了自身的原始标签α，且受正则化参数的影响。 更新后的标签矩阵Y通常需要被重新归一化，以确保每行（代表一个数据点的标签分布）的总和为1。

6、迭代直到收敛

这个更新过程重复进行，直到满足某个收敛条件，例如标签矩阵Y的变化小于某个预设的阈值，或者达到预设的最大迭代次数。

一旦算法收敛，每个未标记数据点的标签被确定为其标签分布中概率最高的那个标签。

在Label Spreading算法中，标签矩阵Y用于表示数据点的标签信息。这个矩阵的结构取决于数据集中的标签数量和数据点的数量。下面是标签矩阵的一般结构和特点：

1.结构

尺寸：标签矩阵Y的尺寸是 N*K ，其中N是数据集中数据点的总数（包括已标记和未标记的数据点），而K是不同标签的数量。

内容:

对于已标记的数据点，每一行对应一个数据点，其中每个元素代表该数据点属于某个标签的概率。在典型的实现中，已标记数据的行会用独热编码（one-hot encoding）表示，即对应该数据点实际标签的位置为1，其余位置为0。

对于未标记的数据点，每一行一开始通常初始化为均匀分布，即每个标签的概率相等，或者根据先验知识进行初始化。

2.示例 假设有一个数据集，其中有3个不同的标签（K = 3），共有5个数据点（N = 5），其中前2个点已标记，后3个点未标记。标签矩阵Y可能如下所示：

在这个例子中，第一行和第二行分别表示第一个和第二个数据点的标签（假设分别属于第一个和第二个类别），而最后三行表示未标记数据点的标签分布，这里初始化为均匀分布。

# Label Spreading
from sklearn.semi_supervised import LabelSpreading

label_spread = LabelSpreading(kernel="knn", alpha=0.8)  # 正则
label_spread.fit(X, labels)

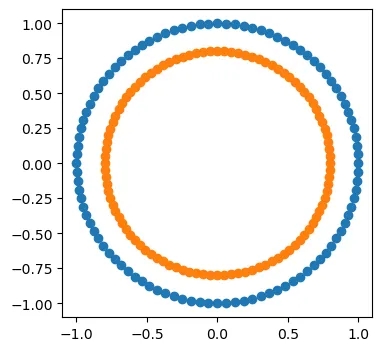
# Label Spreading打标签后的结果
output= np.asarray(label_spread.transduction_)
outer_numbers = np.where(output == outer)[0]
inner_numbers = np.where(output == inner)[0]

plt.figure(figsize=(4, 4))
plt.scatter(X[outer_numbers, 0], X[outer_numbers, 1],)
plt.scatter(X[inner_numbers, 0], X[inner_numbers, 1],)

抓住机遇，狠狠提升自己

随着各行各业进行数字化转型，数据分析能力已经成了职场的刚需能力，这也是这两年CDA数据分析师大火的原因。和领导提建议再说“我感觉”“我觉得”，自己都觉得心虚，如果说“数据分析发现……”，肯定更有说服力。想在职场精进一步还是要学习数据分析的，统计学、概率论、商业模型、SQL，Python还是要会一些，能让你工作效率提升不少。备考CDA数据分析师的过程就是个自我提升的过程。

CDA 考试官方报名入口:https://www.cdaglobal.com/pinggu.html