深入浅出|深度学习算法之BP神经网络 详细公式推导

所谓神经网络，目前用得最广泛的一个定义是“的神经网络是由具有适应性简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应”。

BP(back propagation)神经网络一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。

神经元模型

神经网络中最基本的单元是神经元模型（neuron）。在生物神经网络的原始机制中，每个神经元通常都有多个树突（dendrite），一个轴突（axon）和一个细胞体（cell body），树突短而多分支，轴突长而只有一个；在功能上，树突用于传入其它神经元传递的神经冲动，而轴突用于将神经冲动传出到其它神经元，当树突或细胞体传入的神经冲动使得神经元兴奋时，该神经元就会通过轴突向其它神经元传递兴奋。神经元的生物学结构如下图所示：

一直沿用至今的“M-P神经元模型”正是对这一结构进行了抽象，也称“阈值逻辑单元“，其中树突对应于输入部分，每个神经元收到n个其他神经元传递过来的输入信号，这些信号通过带权重的连接传递给细胞体，这些权重又称为连接权（connection weight）。细胞体分为两部分，前一部分计算总输入值（即输入信号的加权和，或者说累积电平），后一部分先计算总输入值与该神经元阈值的差值，然后通过激活函数（activation function）的处理，产生输出从轴突传送给其它神经元。M-P神经元模型如下图所示：

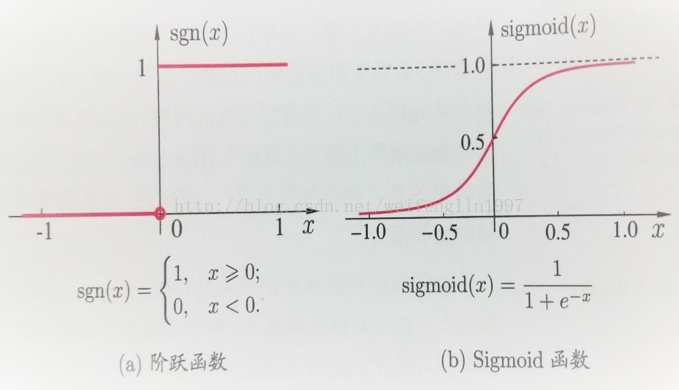
与线性分类十分相似，神经元模型最理想的激活函数也是阶跃函数，即将神经元输入值与阈值的差值映射为输出值1或0，若差值大于零输出1，对应兴奋；若差值小于零则输出0，对应抑制。但阶跃函数不连续，不光滑（定义域内不完全可导），故在M-P神经元模型中，采用Sigmoid函数来近似， Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内，所以也称为挤压函数（squashing function）。

将多个神经元按一定的层次结构连接起来，就得到了神经网络。它是一种包含多个参数的模型，比方说10个神经元两两连接，则有100个参数需要学习（每个神经元有9个连接权以及1个阈值），若将每个神经元都看作一个函数，则整个神经网络就是由这些函数相互嵌套而成。

多次前馈神经网络有三部分组成，分别是输入层(input layer)，隐藏层(hide layer)，输出层(output layer)。隐藏层可以有，也可以没有，输入层和输出层必须要有。没有隐藏层的神经网络是线性的，只能处理线性可分的问题（线性可分问题从二维的角度就是分界线是一条直线，多维就是存在线性超平面将其分类）。一个没有隐藏层且输出层只有一个单元的神经网络就相当于线性的Logistic模型。

感知机与多层网络

感知机（Perceptron）是由两层神经元组成的一个简单模型，但只有输出层是M-P神经元，即只有输出层神经元进行激活函数处理，也称为功能神经元（functionalneuron）；输入层只是接受外界信号（样本属性）并传递给输出层（输入层的神经元个数等于样本的属性数目），而没有激活函数。这样一来，感知机与之前线性回归的思想基本是一样的，都是通过对属性加权与另一个常数求和，再使用sigmoid函数将这个输出值压缩到0-1之间，从而解决分类问题。不同的是感知机的输出层应该可以有多个神经元，从而可以实现多分类问题，同时两个模型所用的参数估计方法十分不同。

给定训练集，则感知机的n+1个参数（n个权重+1个阈值）都可以通过学习得到。阈值Θ可以看作一个输入值固定为-1的哑结点的权重ωn+1，即假设有一个固定输入xn+1=-1的输入层神经元，其对应的权重为ωn+1，这样就把权重和阈值统一为权重的学习了。简单感知机的结构如下图所示：

感知机权重的学习规则如下：对于训练样本（x，y），当该样本进入感知机学习后，会产生一个输出值，若该输出值与样本的真实标记不一致，则感知机会对权重进行调整，若激活函数为阶跃函数，则调整的方法与Logistic回归类似（基于梯度下降法）。

感知机是通过逐个样本输入来更新权重，首先设定好初始权重（一般为随机），逐个地输入样本数据，若输出值与真实标记相同则继续输入下一个样本，若不一致则更新权重，然后再重新逐个检验，直到每个样本数据的输出值都与真实标记相同。容易看出：感知机模型总是能将训练数据的每一个样本都预测正确，和决策树模型总是能将所有训练数据都分开一样，感知机模型很容易产生过拟合问题。

由于感知机模型只有一层功能神经元，因此其功能十分有限，只能处理线性可分的问题，对于这类问题，感知机的学习过程一定会收敛（converge），因此总是可以求出适当的权值。

BP神经网络算法

由上面可以得知：神经网络的学习主要蕴含在权重和阈值中，多层网络使用上面简单感知机的权重调整规则显然不够用了，BP神经网络算法即误差逆传播算法正是为学习多层前馈神经网络而设计，BP神经网络算法是迄今为止最成功的的神经网络学习算法。

一般而言，只需包含一个足够多神经元的隐层，就能以任意精度逼近任意复杂度的连续函数，故下面以训练单隐层的前馈神经网络为例，介绍BP神经网络的算法思想。

上图为一个单隐层前馈神经网络的拓扑结构，BP神经网络算法也使用梯度下降法（gradient descent），以单个样本的均方误差的负梯度方向对权重进行调节。可以看出：BP算法首先将误差反向传播给隐层神经元，调节隐层到输出层的连接权重与输出层神经元的阈值；接着根据隐含层神经元的均方误差，来调节输入层到隐含层的连接权值与隐含层神经元的阈值。BP算法基本的推导过程与感知机的推导过程原理是相同的，下面给出调整隐含层到输出层的权重调整规则的推导过程：

BP算法的最终目标是要最小化整个训练集D上的累积误差

学习率η∈（0，1）控制着沿反梯度方向下降的步长，若步长太大则下降太快容易产生震荡，若步长太小则收敛速度太慢，一般地常把η设置为0.1，有时更新权重时会将输出层与隐含层设置为不同的学习率。BP算法的基本流程如下所示：

BP算法的更新规则是基于每个样本的预测值与真实类标的均方误差来进行权值调节，即BP算法每次更新只针对于单个样例。需要注意的是：BP算法的最终目标是要最小化整个训练集D上的累积误差。

BP神经网络matlab实现的基本步骤

1、数据归一化

2、数据分类，主要包括打乱数据顺序，抽取正常训练用数据、变量数据、测试数据

3、建立神经网络，包括设置多少层网络（一般3层以内既可以，每层的节点数（具体节点数，尚无科学的模型和公式方法确定，可采用试凑法，但输出层的节点数应和需要输出的量个数相等），设置隐含层的传输函数等

4、指定训练参数进行训练，这步非常重要

5、完成训练后，就可以调用训练结果，输入测试数据，进行测试

6、数据进行反归一化

7、误差分析、结果预测或分类，作图等

应用案例

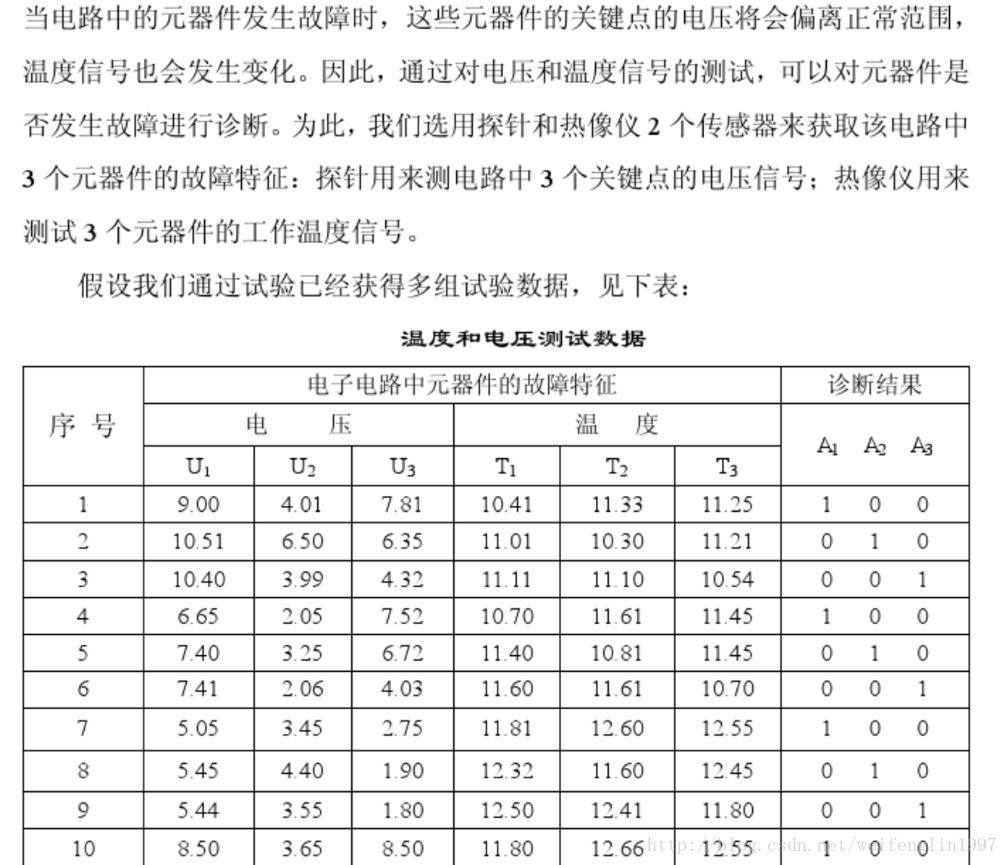
问题的matlab代码：
P=[0.2286 0.1292 0.0720 0.1592 0.1335 0.0733 0.1159 0.0940 0.0522 0.1345 0.0090 0.1260 0.3619 0.0690 0.1828;
   0.2090 0.0947 0.1393 0.1387 0.2558 0.0900 0.0771 0.0882 0.0393 0.1430 0.0126 0.1670 0.2450 0.0508 0.1328;
   0.0442 0.0880 0.1147 0.0563 0.3347 0.1150 0.1453 0.0429 0.1818 0.0378 0.0092 0.2251 0.1516 0.0858 0.0670;
   0.2603 0.1715 0.0702 0.2711 0.1491 0.1330 0.0968 0.1911 0.2545 0.0871 0.0060 0.1793 0.1002 0.0789 0.0909;
   0.3690 0.2222 0.0562 0.5157 0.1872 0.1614 0.1425 0.1506 0.1310 0.0500 0.0078 0.0348 0.0451 0.0707 0.0880;
   0.0359 0.1149 0.1230 0.5460 0.1977 0.1248 0.0624 0.0832 0.1640 0.1002 0.0059 0.1503 0.1837 0.1295 0.0700;
   0.1759 0.2347 0.1829 0.1811 0.2922 0.0655 0.0774 0.2273 0.2056 0.0925 0.0078 0.1852 0.3501 0.1680 0.2668;
   0.0724 0.1909 0.1340 0.2409 0.2842 0.0450 0.0824 0.1064 0.1909 0.1586 0.0116 0.1698 0.3644 0.2718 0.2494;
   0.2634 0.2258 0.1165 0.1154 0.1074 0.0657 0.0610 0.2623 0.2588 0.1155 0.0050 0.0978 0.1511 0.2273 0.3220]';
T=[1 0 0;1 0 0;1 0 0;
   0 1 0;0 1 0;0 1 0;
   0 0 1;0 0 1;0 0 1]';
%输入向量的最大值和最小值
threshold=[0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1;0 1];
net=newff(threshold,[31 3],{'tansig','logsig'},'trainlm');
%训练次数为1000，训练目标为0.01，学习速率为0.1
net.trainParam.epochs=1000;
net.trainParam.goal=0.01;
LP.lr=0.1;
net = train(net,P,T);
%测试数据，和训练数据不一致
P_test=[0.2101 0.0950 0.1298 0.1359 0.2601 0.1001 0.0753 0.0890 0.0389 0.1451 0.0128 0.1590 0.2452 0.0512 0.1319;
        0.2593 0.1800 0.0711 0.2801 0.1501 0.1298 0.1001 0.1891 0.2531 0.0875 0.0058 0.1803 0.0992 0.0802 0.1002;
        0.2599 0.2235 0.1201 0.1171 0.1102 0.0683 0.0621 0.2597 0.2602 0.1167 0.0048 0.1002 0.1521 0.2281 0.3205]';
Y=sim(net,P_test)
%计算训练误差res(P106)
t=[1 0 0;
   0 1 0;
   0 0 1];
error=Y-t
res=norm(error)