 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
一、回顾
介绍了支持向量机的基本概念,线性可分支持向量机的原理以及线性支持向量机的原理,线性可分支持向量机是线性支持向量机的基础。对于线性支持向量机,选择一个合适的惩罚参数,并构造凸二次规划问题:

求得原始问题的对偶问题的最优解,由此可求出原始问题的最优解:

其中 中满足的分量。这样便可以求得分离超平面
中满足的分量。这样便可以求得分离超平面
以及分类决策函数:
线性可分支持向量机算法是线性支持向量机算法的特殊情况。
二、非线性问题的处理方法
在处理非线性问题时,可以通过将分线性问题转化成线性问题,并通过已经构建的线性支持向量机来处理。如下图所示:

(非线性转成线性问题)
通过一种映射可以将输入空间转换到对应的特征空间,体现在特征空间中的是对应的线性问题。核技巧就可以完成这样的映射工作。
1、核函数的定义(摘自《统计机器学习》)
设是输入空间(欧式空间的子集或离散集合),又设为特征空间(希尔伯特空间),如果存在一个从到的映射
使得对所有 ,函数
,函数 满足条件
满足条件
则称 为核函数,为映射函数。
为核函数,为映射函数。
在实际的问题中,通常使用已有的核函数。
2、常用核函数
多项式核函数(Polynomial Kernel Function)
高斯核函数(Gaussian Kernel Function)

三、非线性支持向量机
1、选取适当的核函数和适当的参数,构造原始问题的对偶问题:

求得对应的最优解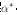 。
。
2、选择 的一个满足的分量,求:
的一个满足的分量,求:
3、构造决策函数
四、实验仿真
对于非线性可分问题,其图像为:

(原始空间中的图像)
MATLAB代码
主程序
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
%% 非线性支持向量机
% 清空内存
clear all;
clc;
% 导入测试数据
A = load('testSetRBF.txt');
%% 区分开训练数据与测试数据
m = size(A);%得到整个数据集的大小
trainA = A(11:m(1,1),:);
testA = A(1:10,:);
% 训练和测试数据集的大小
mTrain = size(trainA);
mTest = size(testA);
% 区分开特征与标签
Xtrain = trainA(:,1:2);
Ytrain = trainA(:,mTrain(1,2))';
Xtest = testA(:,1:2);
Ytest = testA(:,mTest(1,2))';
%% 对偶问题,用二次规划来求解,以求得训练模型
sigma = 0.5;%高斯核中的参数
H = zeros(mTrain(1,1),mTrain(1,1));
for i = 1:mTrain(1,1)
for j = 1:mTrain(1,1)
H(i,j) = GaussianKernalFunction(Xtrain(i,:),Xtrain(j,:),sigma);
H(i,j) = H(i,j)*Ytrain(i)*Ytrain(j);
end
end
f = ones(mTrain(1,1),1)*(-1);
B = Ytrain;
b = 0;
lb = zeros(mTrain(1,1),1);
% 调用二次规划的函数
[x,fval,exitflag,output,lambda] = quadprog(H,f,[],[],B,b,lb);
% 定义C
C = max(x);
% 求解原问题
n = size(x);
k = 1;
for i = 1:n(1,1)
Kernel = zeros(n(1,1),1);
if x(i,1) > 0 && x(i,1)<C
for j = 1:n(1,1)
Kernel(j,:) = GaussianKernalFunction(Xtrain(j,:),Xtrain(i,:),sigma);
Kernel(j,:) = Kernel(j,:)*Ytrain(j);
end
b(k,1) = Ytrain(1,i)-x'*Kernel;
k = k +1;
end
end
b = mean(b);
%% 决策函数来验证训练准确性
trainOutput = zeros(mTrain(1,1),1);
for i = 1:mTrain(1,1)
Kernel_train = zeros(mTrain(1,1),1);
for j = 1:mTrain(1,1)
Kernel_train(j,:) = GaussianKernalFunction(Xtrain(j,:),Xtrain(i,:),sigma);
Kernel_train(j,:) = Kernel_train(j,:)*Ytrain(j);
end
trainOutput(i,1) = x'*Kernel_train+b;
end
for i = 1:mTrain(1,1)
if trainOutput(i,1)>0
trainOutput(i,1)=1;
elseif trainOutput(i,1)<0
trainOutput(i,1)=-1;
end
end
% 统计正确个数
countTrain = 0;
for i = 1:mTrain(1,1)
if trainOutput(i,1) == Ytrain(i)
countTrain = countTrain+1;
end
end
trainCorrect = countTrain./mTrain(1,1);
%% 决策函数来验证测试准确性
testOutput = zeros(mTest(1,1),1);
for i = 1:mTest(1,1)
Kernel_test = zeros(mTrain(1,1),1);
for j = 1:mTrain(1,1)
Kernel_test(j,:) = GaussianKernalFunction(Xtrain(j,:),Xtest(i,:),sigma);
Kernel_test(j,:) = Kernel_test(j,:)*Ytrain(j);
end
testOutput(i,1) = x'*Kernel_train+b;
end
for i = 1:mTest(1,1)
if testOutput(i,1)>0
testOutput(i,1)=1;
elseif testOutput(i,1)<0
testOutput(i,1)=-1;
end
end
% 统计正确个数
countTest = 0;
for i = 1:mTest(1,1)
if testOutput(i,1) == Ytest(i)
countTest = countTest+1;
end
end
testCorrect = countTest./mTest(1,1);
disp(['训练的准确性:',num2str(trainCorrect)]);
disp(['测试的准确性:',num2str(testCorrect)]);
核函数
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
%% 高斯核函数,其中输入x和y都是行向量
function [ output ] = GaussianKernalFunction( x,y,sigma )
output = exp(-(x-y)*(x-y)'./(2*sigma^2));
end
最终的结果为:
注:在这个问题中,有两个参数需要调整,即核参数和惩罚参数,选取合适的参数对模型的训练起着很重要的作用。在程序中,我是指定的参数。这里的程序只是为帮助理解算法的过程。数据分析师培训

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在数据分析、业务决策、科学研究等领域,统计模型是连接原始数据与业务价值的核心工具——它通过对数据的规律提炼、变量关联分析 ...
2026-02-14在SQL查询实操中,SELECT * 与 SELECT 字段1, 字段2,...(指定个别字段)是最常用的两种查询方式。很多开发者在日常开发中,为了 ...
2026-02-14对CDA(Certified Data Analyst)数据分析师而言,数据分析的核心不是孤立解读单个指标数值,而是构建一套科学、完整、贴合业务 ...
2026-02-14在Power BI实操中,函数是实现数据清洗、建模计算、可视化呈现的核心工具——无论是简单的数据筛选、异常值处理,还是复杂的度量 ...
2026-02-13在互联网运营、产品迭代、用户增长等工作中,“留存率”是衡量产品核心价值、用户粘性的核心指标——而次日留存率,作为留存率体 ...
2026-02-13对CDA(Certified Data Analyst)数据分析师而言,指标是贯穿工作全流程的核心载体,更是连接原始数据与业务洞察的关键桥梁。CDA ...
2026-02-13在机器学习建模实操中,“特征选择”是提升模型性能、简化模型复杂度、解读数据逻辑的核心步骤——而随机森林(Random Forest) ...
2026-02-12在MySQL数据查询实操中,按日期分组统计是高频需求——比如统计每日用户登录量、每日订单量、每日销售额,需要按日期分组展示, ...
2026-02-12对CDA(Certified Data Analyst)数据分析师而言,描述性统计是贯穿实操全流程的核心基础,更是从“原始数据”到“初步洞察”的 ...
2026-02-12备考CDA的小伙伴,专属宠粉福利来啦! 不用拼运气抽奖,不用复杂操作,只要转发CDA真题海报到朋友圈集赞,就能免费抱走实用好礼 ...
2026-02-11在数据科学、机器学习实操中,Anaconda是必备工具——它集成了Python解释器、conda包管理器,能快速搭建独立的虚拟环境,便捷安 ...
2026-02-11在Tableau数据可视化实操中,多表连接是高频操作——无论是将“产品表”与“销量表”连接分析产品销量,还是将“用户表”与“消 ...
2026-02-11在CDA(Certified Data Analyst)数据分析师的实操体系中,统计基本概念是不可或缺的核心根基,更是连接原始数据与业务洞察的关 ...
2026-02-11在数字经济飞速发展的今天,数据已成为核心生产要素,渗透到企业运营、民生服务、科技研发等各个领域。从个人手机里的浏览记录、 ...
2026-02-10在数据分析、实验研究中,我们经常会遇到小样本配对数据的差异检验场景——比如同一组受试者用药前后的指标对比、配对分组的两组 ...
2026-02-10在结构化数据分析领域,透视分析(Pivot Analysis)是CDA(Certified Data Analyst)数据分析师最常用、最高效的核心实操方法之 ...
2026-02-10在SQL数据库实操中,字段类型的合理设置是保证数据运算、统计准确性的基础。日常开发或数据分析时,我们常会遇到这样的问题:数 ...
2026-02-09在日常办公数据分析中,Excel数据透视表是最常用的高效工具之一——它能快速对海量数据进行分类汇总、分组统计,将杂乱无章的数 ...
2026-02-09表结构数据作为结构化数据的核心载体,其“获取-加工-使用”全流程,是CDA(Certified Data Analyst)数据分析师开展专业工作的 ...
2026-02-09在互联网产品运营、用户增长的实战场景中,很多从业者都会陷入一个误区:盲目投入资源做推广、拉新,却忽视了“拉新后的用户激活 ...
2026-02-06