2. 描述性统计

上一篇介绍了数据的分类、统计学是什么、以及统计学知识的大分类，本篇我们重点学习描述性统计学。

我们描述一组数据的时候，通常分三个方面描述：集中趋势、离散趋势、分布形状。通俗来说，集中趋势是描述数据集中在什么位置，离散趋势描述的是数据分散的程度，分布形状描述的是数据形状。

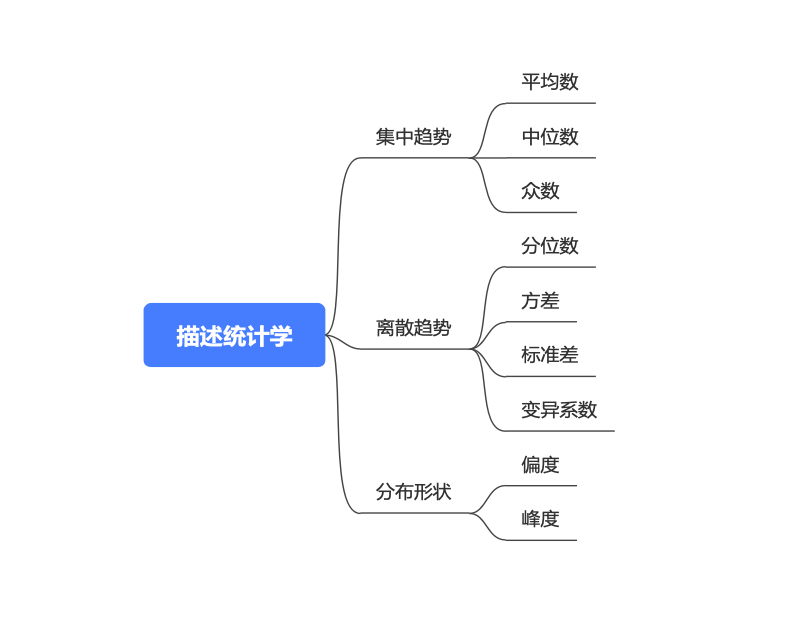
首先，来看描述数据的集中趋势，使用的三个常见的统计量：

平均数

• 算术平均数 算术平均数是n个数求和后除以n得到的结果。广泛应用于各个领域，用于描述和分析数据的平均水平和集中趋势

Excel求算术平均数的函数=AVERAGE(A1:A8)

PS：聪明的你肯定知道把上面8个数据 2,23,4,17,12,12,13,16，用左手复制到你Excel中的A1:A8单元格（记得竖着放！）

用Python求算术平均数

## 使用 numpy 库里的 mean 函数
import numpy as np
data =  [2,23,4,17,12,12,13,16]
print(np.mean(data))
# 12.375

• 几何平均数 几何平均数就是n个数乘积的n次方根。在金融财务、投资和银行业的问题中，几何平均数的应用尤为常见。当你任何时候想确定过去几个连续时期的平均变化率时，都能应用几何平均数。其他通常的应用包括物种总体、农作物产量、污染水平以及出生率和死亡率的变化。（在第8节案例8.1中会举例说明）。 公式如下：

Excel求几何平均数的函数=GEOMEAN(A1:A8)

用Python求几何平均数

# 使用 scipy 库里的 gmean 函数求几何平均数
from scipy import stats as sts
data = [2,23,4,17,12,12,13,16]
print(sts.gmean(data))
# 9.918855683110795

• 调和平均数

n个数的倒数的算术平均数的倒数

Excel求调和平均数的函数=HARMEAN(A1:A8)

Python求调和平均数

# 使用 scipy 库里的 hmean 函数求调和平均数
from scipy import stats as sts
data = [2,23,4,17,12,12,13,16]
print(sts.hmean(data))
# 6.906127821278071

还没看晕吧？我们小结一下，三者的大小排序一般是算术平均值 ≥ 几何平均值 ≥ 调和平均值。另外 数值类数据的均值一般用算术平均值，比例型数据的均值一般用几何平均值，平均速度一般用调和平均数

中位数

中位数是把数据按照顺序排列，处于中间位置的那个数

Excel求中位数的函数=MEDIAN(A1:A8)

Python求中位数

# 使用 numpy 库里的 median 函数求中位数
import numpy as np
data =  [2,23,4,17,12,12,13,16]
print(np.median(data))
# 12.5

众数

众数是一组数据中出现次数最多的变量值。

Excel求众数的函数=MODE(A1:A8)

Python求众数

# 使用 scipy 库里的 mode 函数求众数
from scipy import stats as sts
data =  [2,23,4,17,12,12,13,16]
print(sts.mode(data))
# ModeResult(mode=array([12]), count=array([2]))

以上便是描述数据集中趋势的几个统计量，接下来我们来看描述数据离散趋势的统计量：

分位数

四分位数用3个分位数，将数据等分成4个部分。这3个四分位数，分别位于这组数据升序排序后的25%、50%和75%的位置上。另外，75%分位数与25%分位数的差叫做四分位距。

Excel求分位数的函数=QUARTILE(A1:A8,1) ，括号里面的参数：0代表最小值，1代表25%分位数，2代表50%分位数，3代表75%分位数，4代表最大值，

Python求该组数据的下四分位数与上四分位数

from scipy import stats as sts  
data =  [2,23,4,17,12,12,13,16]
print(sts.scoreatpercentile(data,25)) #25分位数
print(sts.scoreatpercentile(data,75)) #75分位数
10.0
16.25

补充一点，关于描述性统计部分的图表可视化，本系列教程不做展开，唯一值得一提的是箱线图，不论是描述数据、还是判断异常都是你应该掌握的数据分析利器（在第8节案例8.2中会详细举例说明）这里先简单举例如下

用四分位数绘制的箱线图

import seaborn as sns
data = [2,23,4,17,12,12,13,16]
# 使用sns.boxplot()函数绘制箱线图
sns.boxplot(data=data)

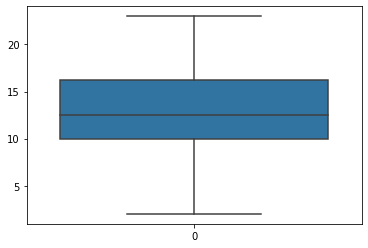箱线图可以很直观地看到：数据的最大值、最小值、以及大部分数据集中在什么区间。

具体来说就是： 异常值、上边缘 Q3+1.5(Q3-Q1)、上四分位数 Q3、中位数 Q2 下四分位数 Q1、下边缘 Q1-1.5(Q3-Q1)

• 极差

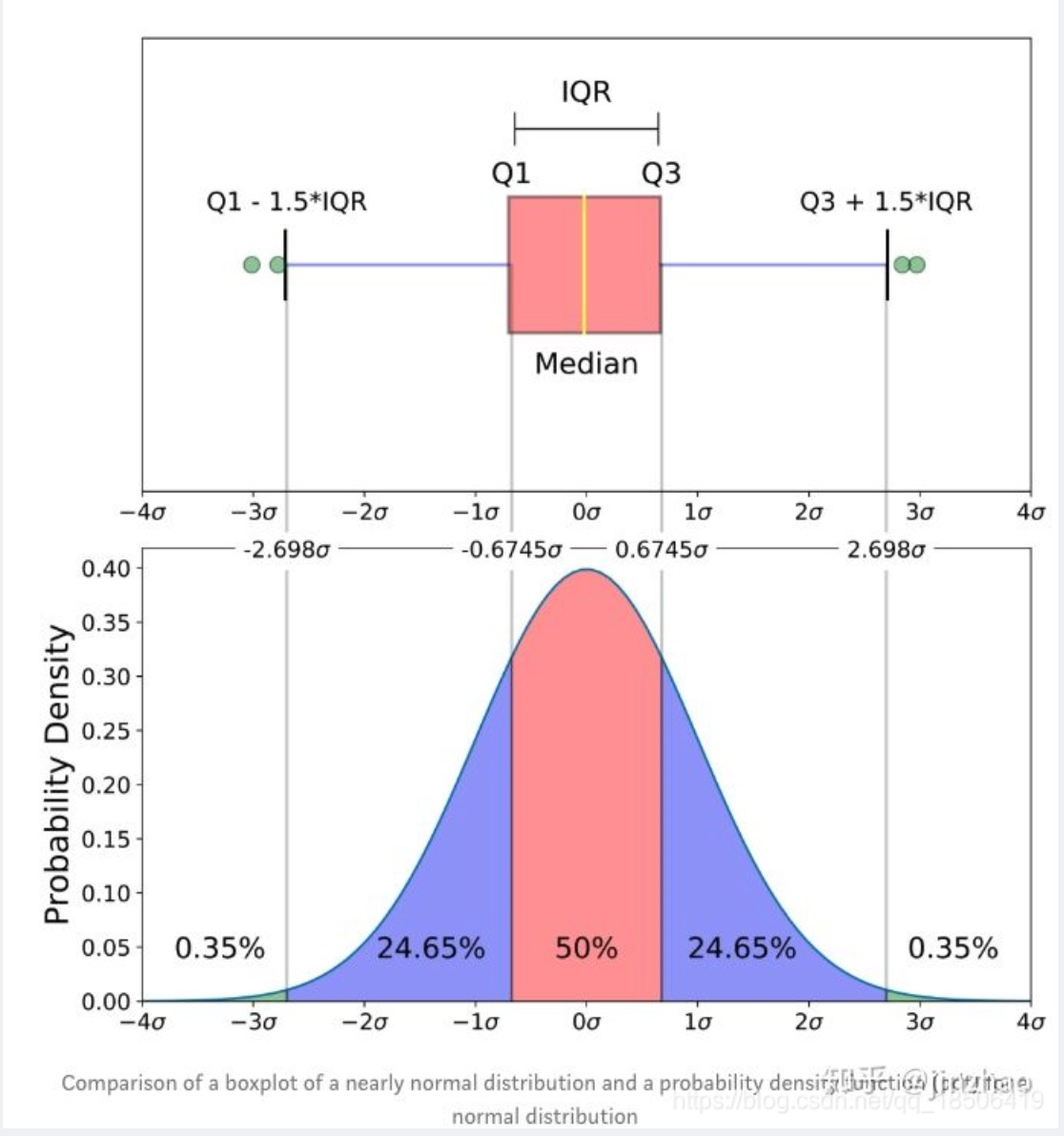
极差又称范围误差或全距，是指一组数据中最大值与最小值的差

Excel求极差的函数=MAX(A1:A8) - MIN(A1:A8)

Python 求极差

import numpy as np
data =  [2,23,4,17,12,12,13,16]
print(np.ptp(data))
# 21

• 四分位距

四分位距是上四分位数与下四分位数之差，一般用表示

Excel求分位数的函数=QUARTILE(A1:A8,3)-QUARTILE(A1:A8,1) Python 求四分位距

from scipy import stats as sts
data =  [2,23,4,17,12,12,13,16]
print(sts.scoreatpercentile(data,75)-sts.scoreatpercentile(data,25))
# 6.25

方差

方差是一组数据中的各数据值与该组数据算术平均数之差的平方的算术平均数。

Excel求方差的函数=VAR(A1:A8)

Python求方差

from scipy import stats as sts
data =  [2,23,4,17,12,12,13,16]
print(sts.tvar(data,ddof = 1))# ddof=1时,分母为n-1;ddof=0时,分母为n
#46.55357142857143

标准差

标准差为方差的开方。总体标准差常用σ表示，样本标准差常用S表示。 Excel求方差的函数=STDEV(A1:A8) Python求标准差:

from scipy import stats as sts
data = [2,23,4,17,12,12,13,16]
print(sts.tstd(data,ddof = 1))# ddof=1时,分母为n-1;ddof=0时,分母为n
# 6.823017765517794

变异系数

对不同变量或不同数组的离散程度进行比较时，如果它们的平均水平和计量单位都相同，才能利用上述指标进行分析，否则需利用变异系数来比较它们的离散程度。

变异系数又称为离散系数，是一组数据中的极差、四分位差或标准差等离散指标与算术平均数的比率。

Excel求变异系数的函数=STDEV(A1:A8)/AVERAGE(A1:A8)

Python求标准差变异系数：

from scipy import stats as sts
data = [2,23,4,17,12,12,13,16]
print(sts.tstd(data)/sts.tmean(data))
# 0.5513549709509329

看完了描述数据离散程度的几个统计量，我们接着看描述数据分布形状的偏度和峰度：

偏度

偏度系数是对分布偏斜程度的测度，通常用SK表示。偏度衡量随机变量概率分布的不对称性，是相对于平均值不对称程度的度量。

当偏度系数为正值时，表示正偏离差数值较大，可以判断为正偏态或右偏态；反之，当偏度系数为负值时，表示负偏离差数值较大，可以判断为负偏态或左偏态。偏度系数的绝对值越大，表示偏斜的程度就越大。

Excel求偏度的函数=SKEW(A1:A8)

Python如何求偏度:

from scipy import stats as sts
data = [2,23,4,17,12,12,13,16]
print(sts.skew(data,bias=False)) # bias=False 代表计算的是总体偏度，bias=True 代表计算的是样本偏度
# -0.21470003988916822

峰度

峰度描述的是分布集中趋势高峰的形态，通常与标准正态分布相比较。在归一化到同一方差时，若分布的形状比标准正态分布更“瘦”、更“高”，则称为尖峰分布；若比标准正态分布更“矮”、更“胖”，则称为平峰分布。

峰度系数是对分布峰度的测度，通常用K表示：

由于标准正态分布的峰度系数为0，所以当峰度系数大于0时为尖峰分布，当峰度系数小于0时为平峰分布。

Excel求峰度的函数 =KURT(A1:A8)

Python如何求峰度:

from scipy import stats as sts
data = [2,23,4,17,12,12,13,16]
print(sts.kurtosis(data,bias=False)) # bias=False 代表计算的是总体峰度，bias=True 代表计算的是样本峰度
# -0.17282884047242897

下期预告：《Python统计学极简入门》第3节 数据分布

这里分享一个你一定用得到的小程序——CDA数据分析师考试小程序。 它是专为CDA数据分析认证考试报考打造的一款小程序。可以帮你快速报名考试、查成绩、查证书、查积分，通过该小程序，考生可以享受更便捷的服务。 扫码加入CDA小程序，与圈内考生一同学习、交流、进步！