作者：小伍哥

来源：小伍哥聊风控

大家好，我是小伍哥，今天给大家分享一个好像有用，好像又没啥用的奇奇怪怪的知识，风控嘛，就是玩儿。

〇、“本福特定律”是什么？

“本福特定律”（Benford's law），也称“本福特法则”，它说明一堆从实际生活得出的数据中，以1为首位数字的数（如12、135、1083首位数字均为1）的出现概率约为总数的三成，接近人们主观直觉得出的期望值1/9的3倍。

推广来说，越大的数，以它为首位数字甚至是首几位数字出现的概率就越低。在十进制首位数字的出现概率中，1最高（30.1%），逐渐递减，9最低（4.6%）。

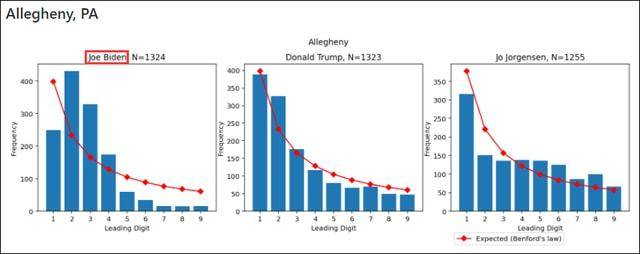
在美国大选中，有人就使用了该定律质疑拜登选票异常，在统计了特朗普和拜登在威斯康星州密尔沃基县470多个选区的得票数首位数字后发现，特朗普的这一曲线较为符合“本福特定律”的曲线，而拜登的曲线形状则出现异常。拜登在包括威斯康星州密尔沃基、伊利诺伊州芝加哥和宾夕法尼亚州阿勒格尼的曲线均不满足“本福特定律”，而与此同时，特朗普在多个地区的曲线却又正好满足或基本满足该定律。

一、基本概念

本福特定律（也称为第一位数法或本福特分布）是一种概率分布，许多统计学的（但不是全部）数据集的第一个数字符合。例如，

15435 首位是 156 首位是 59001 首位是 9199 首位是 19 首位是 9

本福特定律通常可用作欺诈性数据的指标，并可协助审计会计数据。本福特的分布是一种不均匀的分布，较小的数字比较大的数字有更大的出现j可能。

二、数位分布概率第1位数字出现概率10.30120.17630.12540.09750.07960.06770.05880.05190.046

三、本福特分布图

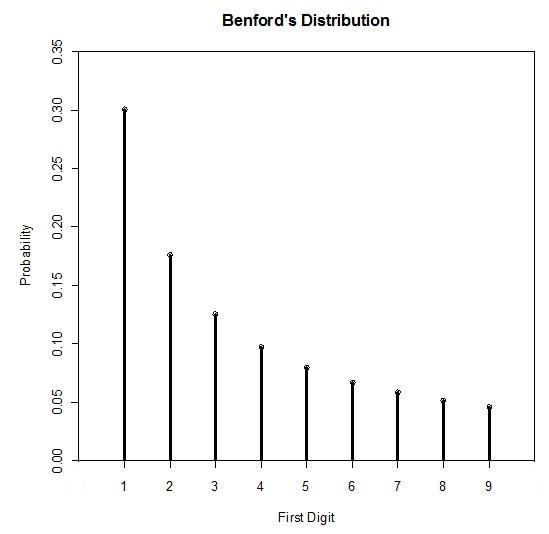
四、本福特分布公式

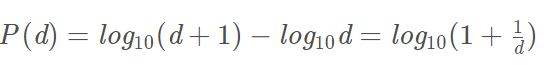
六、本福特定律适用于哪类数据？

需要注意的是，“本福特定律”也有一定的使用条件。首先，数据样本需要尽可能的多，至少要在3000个以上；其次，数据样本跨度要大，比如人的身高就不满足“本福特定律”，因为大多数人身高在1米至2米这一区间；最后，数据样本应是自然的，不能有人为操控，例如手机号码和邮政编码不满足“本福特定律”，因为这些都是1开头或特定数字开头。

也正是因为有特定使用条件，“本福特定律”可用于检查各项数据是否存在造假行为，因为若有人为因素影响数据，所得首位数字的概率及概率曲线图将不符合“本福特定律”。

在大部分情况下，本福特定律可以适用于具有以下特征的数据：

• 具有通过来自多个分布的数字的数学组合形成的值的数据。
• 具有多种数字的数据，例如 具有数百，数千，数万等数值的数据。
• 数据集相当大。
• 数据是右倾斜的，即平均值大于中值，并且分布具有长的右尾而不是对称的。
• 数据没有预定义的最大值或最小值（最小值为零）。

虽然有以上的限制，但实际上在会计中，符合上述特征的数据非常普遍。

七、会计欺诈检测与取证分析

应收账款，应付账款，销售和费用数据均基于两种类型的变量相乘的值，即价格和数量。单独，价格和数量不太可能符合本福特定律，但很可能会成倍增加。这种会计数据也可能是正确的。大公司的交易级会计数据几乎总是会有大量的观察结果。

如果某些会计数据预计符合本福特定律但不符合，则并不一定意味着数据是欺诈性的。然而，这将为进一步调查提供充分的理由。

以下是如何对会计数据执行本福特分布分析的一些示例。

1）大型企业的应付账款数据

分析显示，大型企业的应付几款的数据的数字第一位数字中有很大比例的1。经过仔细检查后发现，与上一个会计期间相比，还有更多的支付支票略高于1000美元。前一期的大部分支票金额低于100美元。

在一起财务调查中，负责的财务官随后受到质疑，他们回答称他们决定汇总金额以试图减少支票。低数字金额的合并是偏离本福特定律的常见解释，使财务官的解释变得合情合理。

经过进一步调查，据透露，该官员正在向他们创建的虚假壳公司写支票。

2）本福特的分析应用于组织的费用数据

最初的本福特分析显示，数据的第一位数字中“非常大”的比例非常大。经过仔细检查，特定费用的许多条目达到45美元。发现费用对于运营组织至关重要，必须经常支付。调查了这笔特殊费用，然后被认为是合法的。

然后将Benford的分析应用于费用数据的副本，但省略了特定的频繁费用。发现排除该特定费用的数据与本福特的分布非常接近。

超越第一个数字推广本福特定律通过查看第一个数字以外的数字，可以增强Benford的分析。

八、广义本福特的分布表

本表的作用是表示分布规则还可以作用在不同的数位上。比如，0出现在第2位的概率是 11.97%，要高于平均值10%。

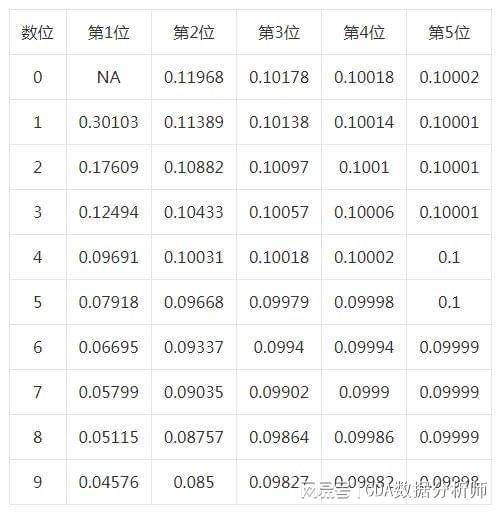
注意：由以上数据可以看出，在广义分布中，数字的出现概率要比第一个数字更加均匀。

九、一般分布公式

根据上面的数据，我们可以得到一般的分布公式

十、上市公司年报净利润数据验证本福特定律

我们用上市公司的利润数据来验证下本福特定律。

我们采用tushare接口获取2019、2020年年报（第4季度）数据，取其中的净利润数据，然后我们只考虑净利润为正的情况。

xxxxxxxxxxbr

# 验证本福特定律import tushare as ts # 股票数据获取的一个包import mathimport matplotlib.pyplot as pltimport pandas as pdfrom functools import reducefrom pylab import *# 这一句让pyplot支持中文显示mpl.rcParams['font.sans-serif'] = ['SimHei']# 获取首位的函数def firstDigital(x): x= round(x) while x >= 10: x //= 10 return x# 首位概率累加def addDigit(lst, digit): lst[digit-1]+=1 return lst# 理论值：每位概率理论值用于对比th_freq=[math.log((x+1)/x, 10) for x in range(1,10)]#分别获得2019，2020年报数据df= ts.get_report_data(2019, 4)# 只取净利润>0的数据，首先进行次数统计freq= reduce(addDigit, map(firstDigital, filter(lambda x:x>0, df['net_profits'])), [0]*9)# 再计算实际概率pr_freq= [x/sum(freq) for x in freq]print(th_freq)print(pr_freq)# 作图plt.title('用上市公司2019年报净利润数据验证本福特定律')plt.xlabel("首位数字")plt.ylabel("概率")plt.xticks(range(9), range(1,10))plt.plot(pr_freq,"r-",linewidth=2, label= '实际值')plt.plot(pr_freq, "go", markersize=5)plt.plot(th_freq,"b-",linewidth=1, label= '理论值')plt.grid(True)plt.legend()plt.show()

xxxxxxxxxxbr # 验证本福特定律brimport tushare as ts # 股票数据获取的一个包brimport mathbrimport matplotlib.pyplot as pltbrimport pandas as pdbrfrom functools import reducebrfrom pylab import *br# 这一句让pyplot支持中文显示brmpl.rcParams['font.sans-serif'] = ['SimHei']br# 获取首位的函数brdef firstDigital(x):br x= round(x)br while x >= 10:br x //= 10br return xbr# 首位概率累加brdef addDigit(lst, digit):br lst[digit-1]+=1br return lstbr# 理论值：每位概率理论值用于对比brth_freq=[math.log((x+1)/x, 10) for x in range(1,10)]br#分别获得2019，2020年报数据brdf= ts.get_report_data(2019, 4)br# 只取净利润>0的数据，首先进行次数统计brfreq= reduce(addDigit, map(firstDigital, filter(lambda x:x>0, df['net_profits'])), [0]*9)br# 再计算实际概率brpr_freq= [x/sum(freq) for x in freq]brprint(th_freq)brprint(pr_freq)br# 作图brplt.title('用上市公司2019年报净利润数据验证本福特定律')brplt.xlabel("首位数字")brplt.ylabel("概率")brplt.xticks(range(9), range(1,10))brplt.plot(pr_freq,"r-",linewidth=2, label= '实际值')brplt.plot(pr_freq, "go", markersize=5)brplt.plot(th_freq,"b-",linewidth=1, label= '理论值')brplt.grid(True)brplt.legend()brplt.show()

xxxxxxxxxxbr br

从图形上看，两者拟合度还是比较高的。据说有些上市公司数据造假就是被用本福特定律查出来的。所以不认真学习的话，造假都造不好。