 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
一、线性回归的概念
对连续型数据做出预测属于回归问题。举个简单的例子:例如我们在知道房屋面积(HouseArea)和卧室的数量(Bedrooms)的情况下要求房屋的价格(Price)。通过一组数据,我们得到了这样的关系:

这样的关系就叫做线性回归方程,其中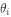 为回归系数。当我们知道房屋面积以及卧室数量时,就可以求出房屋的价格。当然还有一类是非线性回归。
为回归系数。当我们知道房屋面积以及卧室数量时,就可以求出房屋的价格。当然还有一类是非线性回归。
二、基本线性回归
线性回归的目标是要求出线性回归方程,即求出线性回归方程中的回归系数 。我们可以使用平方误差来求线性回归系数。平方误差可以表示为:
。我们可以使用平方误差来求线性回归系数。平方误差可以表示为:

可以使用矩阵表示 。对W求导,得到
。对W求导,得到 。于是令其为0,即得到
。于是令其为0,即得到 的估计
的估计

三、基本线性回归实验
原始的数据

最佳拟合直线
MATLAB代码
主函数
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
%% load Data
A = load('ex0.txt');
X = A(:,1:2);%读取x
Y = A(:,3);
ws = standRegres(X,Y);
%% plot the regression function
x = 0:1;
y = ws(1,:)+ws(2,:)*x;
hold on
xlabel x;
ylabel y;
plot(X(:,2),Y(:,1),'.');
plot(x,y);
hold off
求权重的过程
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
function [ ws ] = standRegres( X, Y )
[m,n] = size(X);
ws = zeros(m,1);
XTX = X'*X;
if det(XTX) == 0
disp('This matrix is singular, cannot do inverse');
end
ws = XTX^(-1) *(X'*Y);
end
四、局部加权线性回归
在线性回归中会出现欠拟合的情况,有些方法可以用来解决这样的问题。局部加权线性回归(LWLR)就是这样的一种方法。局部加权线性回归采用的是给预测点附近的每个点赋予一定的权重,此时的回归系数可以表示为

为给每个点的权重。
LWLR使用核函数来对附近的点赋予更高的权重,常用的有高斯核,对应的权重为

这样的权重矩阵只含对角元素。
五、局部加权线性回归实验
对上组数据做同样的处理:

MATLAB代码
主函数
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
%% load Data
A = load('ex0.txt');
X = A(:,1:2);
Y = A(:,3);
[SX,index] = sort(X);%得到排序和索引
%yHat = lwlrTest(SX, X, Y, 1);
%yHat = lwlrTest(SX, X, Y, 0.01);
%yHat = lwlrTest(SX, X, Y, 0.003);
hold on
xlabel x;
ylabel y;
plot(X(:,2),Y(:,1),'.');
plot(SX(:,2),yHat(:,:));
hold off
LWLR
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
function [ output ] = lwlr( testPoint, X, Y, k )
[m,n] = size(X);%得到数据集的大小
weight = zeros(m,m);
for i = 1:m
diff = testPoint - X(i,:);
weight(i,i) = exp(diff * diff'./(-2*k^2));
end
XTX = X'*(weight * X);
if det(XTX) == 0
disp('his matrix is singular, cannot do inverse');
end
ws = XTX^(-1) * (X' * (weight * Y));
output = testPoint * ws;
end
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
function [ y ] = lwlrTest( test, X, Y, k )
[m,n] = size(X);
y = zeros(m,1);
for i = 1:m
y(i,:) = lwlr(test(i,:), X, Y, k);
end
end
当k=1时是欠拟合,当k=0.003时是过拟合,选择合适的很重要。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在数据分析、业务决策、科学研究等领域,统计模型是连接原始数据与业务价值的核心工具——它通过对数据的规律提炼、变量关联分析 ...
2026-02-14在SQL查询实操中,SELECT * 与 SELECT 字段1, 字段2,...(指定个别字段)是最常用的两种查询方式。很多开发者在日常开发中,为了 ...
2026-02-14对CDA(Certified Data Analyst)数据分析师而言,数据分析的核心不是孤立解读单个指标数值,而是构建一套科学、完整、贴合业务 ...
2026-02-14在Power BI实操中,函数是实现数据清洗、建模计算、可视化呈现的核心工具——无论是简单的数据筛选、异常值处理,还是复杂的度量 ...
2026-02-13在互联网运营、产品迭代、用户增长等工作中,“留存率”是衡量产品核心价值、用户粘性的核心指标——而次日留存率,作为留存率体 ...
2026-02-13对CDA(Certified Data Analyst)数据分析师而言,指标是贯穿工作全流程的核心载体,更是连接原始数据与业务洞察的关键桥梁。CDA ...
2026-02-13在机器学习建模实操中,“特征选择”是提升模型性能、简化模型复杂度、解读数据逻辑的核心步骤——而随机森林(Random Forest) ...
2026-02-12在MySQL数据查询实操中,按日期分组统计是高频需求——比如统计每日用户登录量、每日订单量、每日销售额,需要按日期分组展示, ...
2026-02-12对CDA(Certified Data Analyst)数据分析师而言,描述性统计是贯穿实操全流程的核心基础,更是从“原始数据”到“初步洞察”的 ...
2026-02-12备考CDA的小伙伴,专属宠粉福利来啦! 不用拼运气抽奖,不用复杂操作,只要转发CDA真题海报到朋友圈集赞,就能免费抱走实用好礼 ...
2026-02-11在数据科学、机器学习实操中,Anaconda是必备工具——它集成了Python解释器、conda包管理器,能快速搭建独立的虚拟环境,便捷安 ...
2026-02-11在Tableau数据可视化实操中,多表连接是高频操作——无论是将“产品表”与“销量表”连接分析产品销量,还是将“用户表”与“消 ...
2026-02-11在CDA(Certified Data Analyst)数据分析师的实操体系中,统计基本概念是不可或缺的核心根基,更是连接原始数据与业务洞察的关 ...
2026-02-11在数字经济飞速发展的今天,数据已成为核心生产要素,渗透到企业运营、民生服务、科技研发等各个领域。从个人手机里的浏览记录、 ...
2026-02-10在数据分析、实验研究中,我们经常会遇到小样本配对数据的差异检验场景——比如同一组受试者用药前后的指标对比、配对分组的两组 ...
2026-02-10在结构化数据分析领域,透视分析(Pivot Analysis)是CDA(Certified Data Analyst)数据分析师最常用、最高效的核心实操方法之 ...
2026-02-10在SQL数据库实操中,字段类型的合理设置是保证数据运算、统计准确性的基础。日常开发或数据分析时,我们常会遇到这样的问题:数 ...
2026-02-09在日常办公数据分析中,Excel数据透视表是最常用的高效工具之一——它能快速对海量数据进行分类汇总、分组统计,将杂乱无章的数 ...
2026-02-09表结构数据作为结构化数据的核心载体,其“获取-加工-使用”全流程,是CDA(Certified Data Analyst)数据分析师开展专业工作的 ...
2026-02-09在互联网产品运营、用户增长的实战场景中,很多从业者都会陷入一个误区:盲目投入资源做推广、拉新,却忽视了“拉新后的用户激活 ...
2026-02-06