 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
1、线性回归
线性回归就是使用下面的预测函数预测未来观测量:
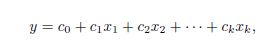
其中,x1,x2,...,xk都是预测变量(影响预测的因素),y是需要预测的目标变量(被预测变量)。
线性回归模型的数据来源于澳大利亚的CPI数据,选取的是2008年到2011年的季度数据。
rep函数里面的第一个参数是向量的起始时间,从2008-2010,第二个参数表示向量里面的每个元素都被4个小时间段。
year <- rep(2008:2010, each=4)
quarter <- rep(1:4, 3)
cpi <- c(162.2, 164.6, 166.5, 166.0,
166.2, 167.0, 168.6, 169.5,
171.0, 172.1, 173.3, 174.0)
plot函数中axat=“n”表示横坐标刻度的标注是没有的
plot(cpi, xaxt="n", ylab="CPI", xlab="")
绘制横坐标轴
axis(1, labels=paste(year,quarter,sep="Q"), at=1:12, las=3)
接下来,观察CPI与其他变量例如‘year(年份)’和‘quarter(季度)’之间的相关关系。
cor(year,cpi)
cor(quarter,cpi)
输出如下:
cor(quarter,cpi)
[1] 0.3738028
cor(year,cpi)
[1] 0.9096316
cor(quarter,cpi)
[1] 0.3738028
由上图可知,CPI与年度之间的关系是正相关,并且非常紧密,相关系数接近1;而它与季度之间的相关系数大约为0.37,只是有着微弱的正相关,关系并不明显。
然后使用lm()函数建立一个线性回归模型,其中年份和季度为预测因素,CPI为预测目标。
建立模型fit
fit <- lm(cpi ~ year + quarter)
fit
输出结果如下:
Call:
lm(formula = cpi ~ year + quarter)
Coefficients:
(Intercept) year quarter
-7644.488 3.888 1.167
由上面的输出结果可以建立以下模型公式计算CPI:
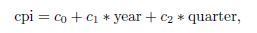
其中,c0、c1和c2都是模型fit的参数分别是-7644.488、3.888和1.167。因此2011年的CPI可以通过以下方式计算:
(cpi2011 <-fit$coefficients[[1]] + fit$coefficients[[2]]*2011 +
fit$coefficients[[3]]*(1:4))
输出的2011年的季度CPI数据分别是174.4417、175.6083、176.7750和177.9417。
模型的具体参数可以通过以下代码查看:
查看模型的属性
attributes(fit)
$names
[1] "coefficients" "residuals" "effects" "rank" "fitted.values"
[6] "assign" "qr" "df.residual" "xlevels" "call"
[11] "terms" "model"
$class
[1] "lm"
模型的参数
fit$coefficients
观测值与拟合的线性模型之间的误差,也称为残差
residuals(fit)
1 2 3 4 5 6 7
-0.57916667 0.65416667 1.38750000 -0.27916667 -0.46666667 -0.83333333 -0.40000000
8 9 10 11 12
-0.66666667 0.44583333 0.37916667 0.41250000 -0.05416667
除了将数据代入建立的预测模型公式中,还可以通过使用predict()预测未来的值。
输入预测时间
data2011 <- data.frame(year=2011, quarter=1:4)
cpi2011 <- predict(fit, newdata=data2011)
设置散点图上的观测值和预测值对应点的风格(颜色和形状)
style <- c(rep(1,12), rep(2,4))
plot(c(cpi, cpi2011), xaxt="n", ylab="CPI", xlab="", pch=style, col=style)
标签中sep参数设置年份与季度之间的间隔
axis(1, at=1:16, las=3,
labels=c(paste(year,quarter,sep="Q"), "2011Q1", "2011Q2", "2011Q3", "2011Q4"))
预测结果如下:

上图中红色的三角形就是预测值。
2、Logistic回归
Logistic回归是通过将数据拟合到一条线上并根据简历的曲线模型预测事件发生的概率。可以通过以下等式来建立一个Logistic回归模型:

其中,x1,x2,...,xk是预测因素,y是预测目标。令
,上面的等式被转换成:
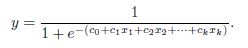
使用函数glm()并设置响应变量(被解释变量)服从二项分布(family='binomial,'link='logit')建立Logistic回归模型,更多关于Logistic回归模型的内容可以通过以下链接查阅:
· R Data Analysis Examples - Logit Regression
· 《LogisticRegression (with R)》
3、广义线性模型
广义线性模型(generalizedlinear model, GLM)是简单最小二乘回归(OLS)的扩展,响应变量(即模型的因变量)可以是正整数或分类数据,其分布为某指数分布族。其次响应变量期望值的函数(连接函数)与预测变量之间的关系为线性关系。因此在进行GLM建模时,需要指定分布类型和连接函数。这个建立模型的分布参数包括binomaial(两项分布)、gaussian(正态分布)、gamma(伽马分布)、poisson(泊松分布)等。
广义线性模型可以通过glm()函数建立,使用的数据是包‘TH.data’自带的bodyfat数据集。
data("bodyfat", package="TH.data")
myFormula <- DEXfat ~ age + waistcirc + hipcirc + elbowbreadth + kneebreadth
设置响应变量服从正态分布,对应的连接函数服从对数分布
bodyfat.glm <- glm(myFormula, family = gaussian("log"), data = bodyfat)
预测类型为响应变量
pred <- predict(bodyfat.glm, type="response")
plot(bodyfat$DEXfat, pred, xlab="Observed Values", ylab="Predicted Values")
abline(a=0, b=1)
预测结果检验如下图所示:

由上图可知,模型虽然也有离群点,但是大部分的数据都是落在直线上或者附近的,也就说明模型建立的比较好,能较好的拟合数据。
4、非线性回归
如果说线性模型是拟合拟合一条最靠近数据点的直线,那么非线性模型就是通过数据拟合一条曲线。在R中可以使用函数nls()建立一个非线性回归模型,具体的使用方法可以通过输入'?nls()'查看该函数的文档。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在数据分析实战中,我们经常会遇到“多指标冗余”的问题——比如分析企业经营状况时,需同时关注营收、利润、负债率、周转率等十 ...
2026-02-04在数据分析场景中,基准比是衡量指标表现、评估业务成效、对比个体/群体差异的核心工具,广泛应用于绩效评估、业务监控、竞品对 ...
2026-02-04业务数据分析是企业日常运营的核心支撑,其核心价值在于将零散的业务数据转化为可落地的业务洞察,破解运营痛点、优化业务流程、 ...
2026-02-04在信贷业务中,违约率是衡量信贷资产质量、把控信用风险、制定风控策略的核心指标,其统计分布特征直接决定了风险定价的合理性、 ...
2026-02-03在数字化业务迭代中,AB测试已成为验证产品优化、策略调整、运营活动效果的核心工具。但多数业务场景中,单纯的“AB组差异对比” ...
2026-02-03企业战略决策的科学性,决定了其长远发展的格局与竞争力。战略分析方法作为一套系统化、专业化的思维工具,为企业研判行业趋势、 ...
2026-02-03在统计调查与数据分析中,抽样方法分为简单随机抽样与复杂抽样两大类。简单随机抽样因样本均匀、计算简便,是基础的抽样方式,但 ...
2026-02-02在数据驱动企业发展的今天,“数据分析”已成为企业经营决策的核心支撑,但实践中,战略数据分析与业务数据分析两个概念常被混淆 ...
2026-02-02在数据驱动企业发展的今天,“数据分析”已成为企业经营决策的核心支撑,但实践中,战略数据分析与业务数据分析两个概念常被混淆 ...
2026-02-02B+树作为数据库索引的核心数据结构,其高效的查询、插入、删除性能,离不开节点间指针的合理设计。在日常学习和数据库开发中,很 ...
2026-01-30在数据库开发中,UUID(通用唯一识别码)是生成唯一主键、唯一标识的常用方式,其标准格式包含4个短横线(如550e8400-e29b-41d4- ...
2026-01-30商业数据分析的价值落地,离不开标准化、系统化的总体流程作为支撑;而CDA(Certified Data Analyst)数据分析师,作为经过系统 ...
2026-01-30在数据分析、质量控制、科研实验等场景中,数据波动性(离散程度)的精准衡量是判断数据可靠性、稳定性的核心环节。标准差(Stan ...
2026-01-29在数据分析、质量检测、科研实验等领域,判断数据间是否存在本质差异是核心需求,而t检验、F检验是实现这一目标的经典统计方法。 ...
2026-01-29统计制图(数据可视化)是数据分析的核心呈现载体,它将抽象的数据转化为直观的图表、图形,让数据规律、业务差异与潜在问题一目 ...
2026-01-29箱线图(Box Plot)作为数据分布可视化的核心工具,能清晰呈现数据的中位数、四分位数、异常值等关键统计特征,广泛应用于数据分 ...
2026-01-28在回归分析、机器学习建模等数据分析场景中,多重共线性是高频数据问题——当多个自变量间存在较强的线性关联时,会导致模型系数 ...
2026-01-28数据分析的价值落地,离不开科学方法的支撑。六种核心分析方法——描述性分析、诊断性分析、预测性分析、规范性分析、对比分析、 ...
2026-01-28在机器学习与数据分析领域,特征是连接数据与模型的核心载体,而特征重要性分析则是挖掘数据价值、优化模型性能、赋能业务决策的 ...
2026-01-27关联分析是数据挖掘领域中挖掘数据间潜在关联关系的经典方法,广泛应用于零售购物篮分析、电商推荐、用户行为路径挖掘等场景。而 ...
2026-01-27