总是说XX的样本量就够了，可是为什么呢？

如何决定样本量，是一个老生常谈的话题，也有很多相关文章。然而翻看相关文章，就会发现介绍选多少合适的比较多，而介绍为什么这么选就合适的却比较少。

相信很多用研同学都听过这句著名的话：

根据尼尔森关于可用性测试的经典理论，6-8人便可以找到产品80%以上的可用性问题。

但是……为啥呢？当有“无知的”地球人问：为什么6-8人就能发现80%以上的问题时，难道我们要理直气壮的说：因为是尼尔森说的么……

在样本量选择上似乎有一些“约定俗成”的规定。比如：可用性测试5-8人，问卷调研大约200-500份等等……但是，当需要和地球人理论时，单单的“约定俗成”却没有足够的说服力。不如让我们一起来看看这些“约定俗成”背后的科学道理，让自己更有底气。

1. 为什么说可用性测试5-8个人就够？

俗话说“8个用户可以发现80%的问题”。其实这句话并不完整，完整的说法应该是：

8个人可以80%的概率发现发生可能性大于18%的问题。

这话太绕了，尝试用人话解释一下：如果某个APP中存在一个BUG，100个人用，50个人用都会遇到，那么我们至少有80%的可能性发现。只要可能遇到的人大于18个（发生可能性大于18%），我们都至少有80%的可能性发现。但如果这个BUG只有5个人可会遇到，那么能发现的概率就要低于80%了。

之所以这么说，背后的原理是这样一个公式：

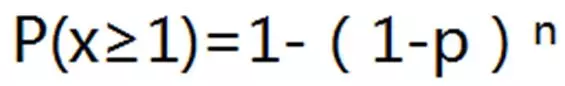
（P（X≥1）是在n次尝试中事件至少发生1次的概率，p是某事件的概率）

前辈们根据这个公式总结出了下表：

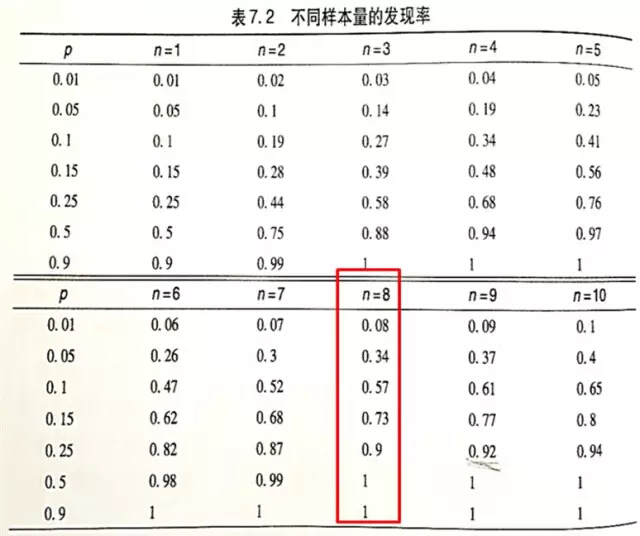
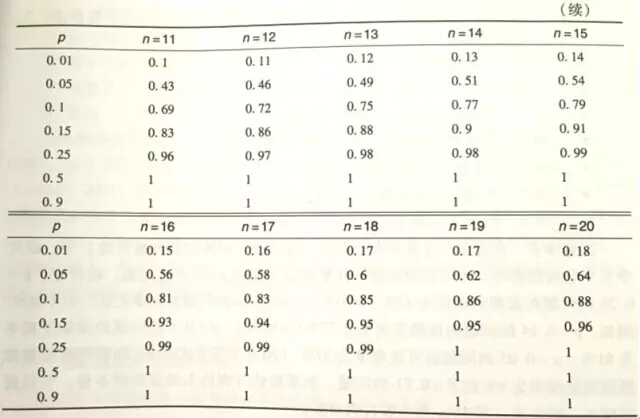
资料来源：《用户体验度量》Jeff Sauro，James R.Lewis著，机械工业出版社，P134-135

从表中可以看出，决定样本量涉及到两个因素：一个是确定程度，一个是问题发生的概率。

再来具体看一看我们常说的“8个人”。

当选择8个人进行测试时，可以100%发现发生概率大于50%的问题，90%的可能性发现发生概率大于25%的问题，73%的可能性发现发生概率大于15%的问题。

就好像天气预报员说：100%的确定明天的降水概率大于50%，90%的确定明天的降水概率大于25%。

等等…这样的话会不会被质疑：8个人只能90%发现发生概率大于25%的问题，那发生概率低于25%的问题怎么办？就不重要了么？

不如让我们再来看看尼尔森关于钓鱼的比喻：

假设你有好多个池塘可以钓鱼，一些鱼比另一些鱼更容易抓到。所以，如果你有10小时，你会花10个小时都在一个池塘里钓鱼，还是花5个小时在一个池塘上、花另外的5个小时在另一个池塘上呢？ 为使抓到的鱼数量最大化，你应该在两个池塘上都花一些时间，以便从每个池塘里都钓到容易钓的鱼。

一次何必找那么多用户，少做几个用户先把发生率高的问题get了，版本更新以后再继续找用户去get发生率高的问题，省时省力效果佳。

这样是不是就可以完整的证明我们可用性测试做5-8个人的观点了呢。

2. 问卷调研，样本量选多少？

在做问卷调研的时候，如何估计样本量？众所周知有一个公式：

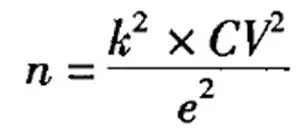
但是这个公式存在一个问题：我要是连总体方差（CV2）都能知道，还做个毛线调研。

如果想估算总体方差，需要先选取一批人进行测试，得到一个样本方差，用样本方差代替总体方差，这在现实工作中显然难以实现。于是为了便于计算，伟大的前辈对公式进行了转换：

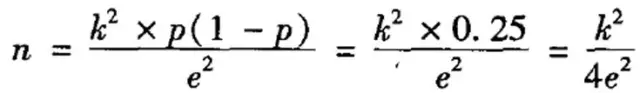
资料来源：《社会研究方法》仇立平著，重庆大学出版社，P137

作者说这一转换是根据“推论总体比例或百分比的原理”进行的。姑且不去管这个转换原理是什么，这个公式我们可以这样来理解：当p=0.5的时候，总体的差异性最大。因为p=0.5表示两种情况出现的概率是相等的。比如一个群体中男生和女生出现的概率都是0.5，说明男女人数相等。这种情况下，这个群体的性别差异是最大的。

由于总体差异越大，需要的样本量就越大。我们面对任何总体的时候，都可以假设“这是一个差异性最大的总体”，来计算我们所需要的样本量。因此，把p=0.5代入，就简化出了一个可以供我们轻松计算样本量的公式。

如果想看到总体不同差异所对应的样本量，前人还总结了这样一个表：

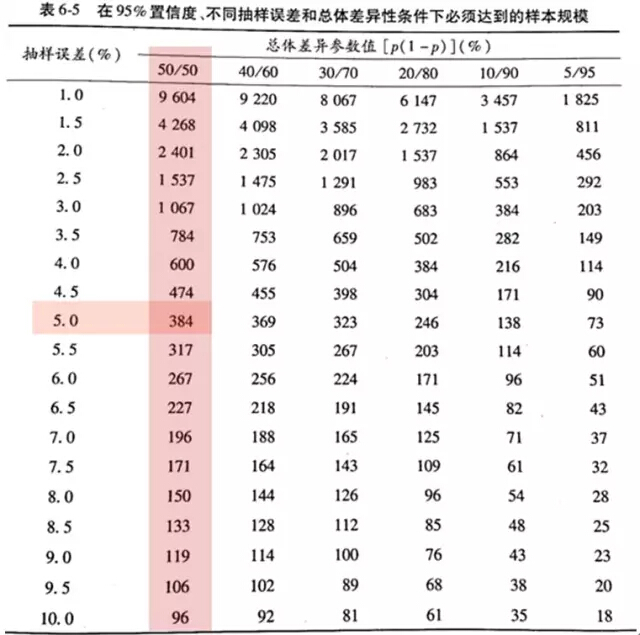
资料来源：《社会研究方法》仇立平著，重庆大学出版社，P137

因此假设总体差异性最大的情况下，在习惯使用的5%误差档，300多的样本也就可以了。

当然，在具体使用过程中，并不用查表那么麻烦。有一个著名的计算样本量的网站，直接去算就OK了。

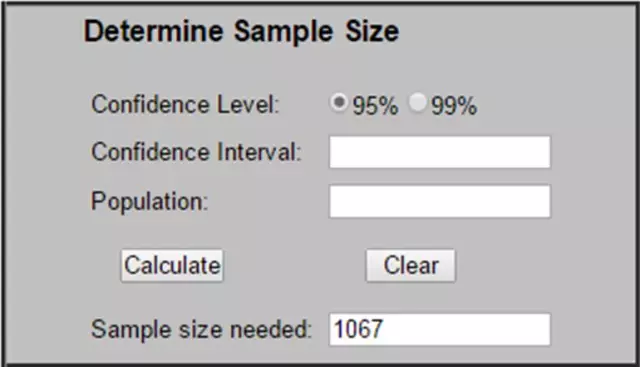
http://www.surveysystem.com/sscalc.htm

3.用户量越大，需调研人数越多？

首先，总体规模会对样本量有影响。当总体规模比较小的时候，对样本量影响较大。但是当总体规模达到一定程度以后，对样本量增加的需求是较小的。

我们往往调查所涉及到的总体不是无限总体，产品的用户人数都是一个有限的数量。因此在计算所需样本量的时候，为了更精确可以加入变量“总体规模”，公式大概长成这个样子：

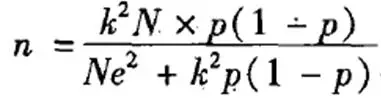
然而这不是重点，重点是通过这个公式可以计算出，不同总体规模所需要的样本量大致如下：

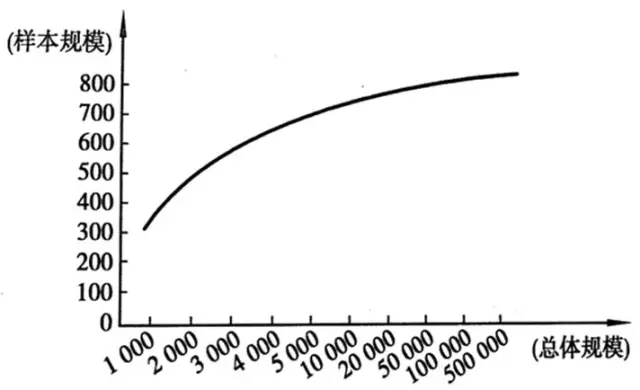
由此可以看出，当总体规模在1万以下时，随着总体规模上升，所需样本量增加比较大。但是当总体规模在1万以上时，规模再变大，所需样本人数的增长变得缓慢。

为了得到更准确的答案，我们不妨用计算样本量的网址自己来算一下。假设置信区间为±3个标准差。计算结果如下：

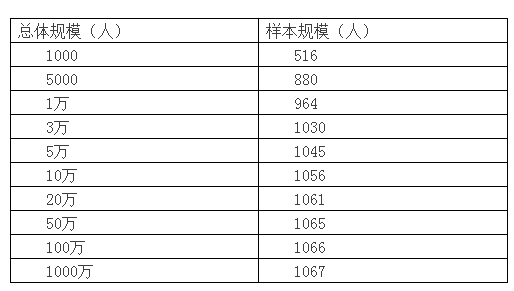
如果再有人说：我们是亿级的产品，1000人怎么能代表我们的用户？

就可以理直气壮的告诉他：

总体规模10万以上和10万所需要的样本量并没有什么区别呢。

样本量选多少合适，对于调研本身而言或许不是个问题。但是当我们想推动调研结果的时候，样本量却很容易遭到对方质疑。可能是几百个人的答案看起来容易让人觉得不靠谱，也可能因为样本量是最容易质疑的一个因素……

无论如何，多了解一些背后的原因，让自己更有底气，或许才能更好地说服别人。