特征值和特征向量的详细计算及几何意义

矩阵特征值与特征向量在机器学习算法中经常会用到，每次出现都有着其独特的意义，如果不能深入理解特征值和特征向量两个概念，对我们机器学习的实际应用会有很大影响。小编今天整理了特征值和特征向量的概念计算以及几何意义，希望对大家机器学习有所帮助。

一、特征值和特征向量的概念和计算

设A是n阶方阵，如果存在常数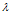及非零n向量x，使得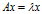，则称是矩阵A的特征值，x是A属于特征值的特征向量。给定n阶矩阵A，行列式

的结果是关于的一个多项式，成为矩阵A的特征多项式，该特征多项式构成的方程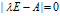称为矩阵A的特征方程。

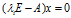
　　定理：n阶矩阵A的n个特征值就是其特征方程的n个跟；而A的属于特征值的特征向量就是其次线性方程的非零解。

二、特征值和特征向量的几何意义

我们先记线性变换一个T（Transformation）为，容易知道矩阵代表一个线性变换，可以做升维降维，放大缩小以及旋转的线性变换，而对于方阵而言，是不存在升维降维的。即一个方阵其对向量的线性变换为伸长收缩或者旋转。

在为基向量的空间下有个向量:

对随便左乘一个矩阵，即对进行一个线性变换。

调整下的方向，使其特殊一点。

可以观察到，调整后的和在同一直线上，只是的长度相对的长度变长了。

此时，我们就称是的特征向量，而的长度是的长度的倍，就是特征值。

即