用SAS模拟随机数据 求PIE值

刚刚看到一本好书《统计模拟》作者叫罗斯[英文：Sheldon M. Ross. Simulation(4th Ed).Elsevier Inc..2006 ]. 顾名思义，这是一本描述怎么利用模拟一些符合统计学理论的数据，用途很广，也就是说实际中的任何数据的分布都符合某种统计学模型，于是在没有得到真实数据之前，数据分析师可以通过模拟数据来研究这些现实中的问题。如果通过模拟来研究未知问题，可以说得上是研究境界很高了。总不能拿到一些实际数据，画个好看的图，就觉得自己可画遍天下了吧。

由于自己不是统计出生，但是受过统计学老师的循循教诲，凡事从简单开始。于是goolge了一下，当当中有这本书的中文介绍：

本书系统阐述了统计模拟的一些实用方法和技术。在对概率的基本知识进行了简单的回顾之后，介绍如何利用计算机产生随机数以及如何利用这些随机数产生任意分布的随机变量、随机过程等。然后讨论了一些分析统计数据的方法和技术。如Bootstrap（自助法）、方差缩减技术等。接着讲述了如何利用统计模拟来判断所选的随机模型是否拟合实际的数据。最后介绍MCMC及一些最新发展的统计模拟技术和论题，如随机序列函数和随机子集函数的评估。本书在每章的最后还提供了不同难度的习题。本书可作为高等院校数学、统计学、科学计算、保险学、精算学等专业的教材，也可供工程技术人员和应用工作者参考。

一看有很多不懂的术语，顿时心生敬仰，后面写着可以供“工程技术人员”参考，很显然，我可以是这本书的读者。全书近300页，在今天剩下不多的时间内，很显然，我决定不去看这本书，哪怕是一个字。还是老师的教导，从简单开始。google到一个有趣的问题：用统计模拟计算圆周率pie值。Forcode提供了一种用excel求解pie的详细过程，然后有人用Mathematica计算出来了。Hujiangtang很仔细的阐述了什么是随机数？什么是蒙特卡罗模拟？为什么选择SAS做蒙特卡罗模拟？SAS怎么做出来这些，还可以做哪些哪些分布…… 其中引用这个用统计模拟计算pie的例子和上述用excel和mathematica的方法，可是就是不提供解决这个问题的SAS代码，在我看来，这是不可想象，我很仔细的找了半天，未果，于是我自己编了下列代码，用SAS来实现模拟pie值。

借用别人写的原理和图来说明一下，

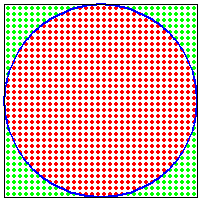
原理很简单：

1）生成随机数——生成n个均匀落在正方形内的点；

2）对落在正方形内的n个点，数一数正好落在圆里面的点的个数，假设为k（另外n-k个点就落在圆外面的正方形区域内）。数据分析师培训

3）k/n就可以大致认为是圆的面积与正方形的面积之比，另其等于pai/4，就可以求出圆周率∏的估计值。n越大，算出来的pai­值越精确

SAS实现代码：

%let num_s=10000;
data ex;
do i= 1 to &num_s.;
x=ranuni(0); y=ranuni(0);
area=sqrt(x**2+y**2);
output;
end;
run;

proc sort;
by area;
run;

data ex2;
set ex;
y1=.;y2=.;
num=_n_;
if area<=1 then y1=y ; else y2=y;
if area>1 and lag(area)<=1 then
do;
pie=(num*4)/&num_s.;
sas_pie=constant(‘pi’);
put pie= sas_pie=;
end;
run;
FILENAME file “c:\simulation.png”;
goptions reset=all hsize=8cm vsize=8cm  noborder device=png gsfname=file;;
symbol1 v=dot color=’red’ height=0.3;
symbol2 v=dot color=’blue’ height=0.3;
proc gplot;
plot  y1*x y2*x/overlay noaxis;
run;
quit;

模拟的点数为 100时pie=3；1000时，pie=3.068； 10000时， pie=3.1392；100000时pie=3.13543；1000000时，pie=3.141524，10000000时，pie=3.1418008。当然SAS也提供了pie的精确值供使用，使用函数constant就可以：sas_pie=constant(‘pi’); 值为：3.1415926536。上面的示例只是为了演示统计模拟的使用，其实SAS提供了很多种随机函数，几乎所有分布的随机函数供大家使用，这里就不详述了.CDA数据分析师培训