一、分类算法中的损失函数
在分类算法中，损失函数通常可以表示成损失项和正则项的和，即有如下的形式：
其中，L(mi(w))为损失项，R(w)为正则项。mi的具体形式如下：
对于损失项，主要的形式有：
0-1损失
Log损失
Hinge损失
指数损失
感知损失
1、0-1损失函数
在分类问题中，可以使用函数的正负号来进行模式判断，函数值本身的大小并不是很重要，0-1损失函数比较的是预测值fw(x(i))与真实值y(i)的符号是否相同，0-1损失的具体形式如下：
以上的函数等价于下述的函数：
0-1损失并不依赖m值的大小，只取决于m的正负号。0-1损失是一个非凸的函数，在求解的过程中，存在很多的不足，通常在实际的使用中将0-1损失函数作为一个标准，选择0-1损失函数的代理函数作为损失函数。
Log损失是0-1损失函数的一种代理函数，Log损失的具体形式如下：
运用Log损失的典型分类器是Logistic回归算法。
对于Logistic回归算法，分类器可以表示为：
为了求解其中的参数w，通常使用极大似然估计的方法，具体的过程如下：
1、似然函数
其中，
2、log似然
3、需要求解的是使得log似然取得最大值的w。将其改变为最小值，可以得到如下的形式：
由于Log损失的具体形式为：
Logistic回归与Log损失具有相同的形式，故两者是等价的。Log损失与0-1损失的关系可见下图。
Hinge损失是0-1损失函数的一种代理函数，Hinge损失的具体形式如下：
运用Hinge损失的典型分类器是SVM算法。
对于软间隔支持向量机，允许在间隔的计算中出现少许的误差
，其优化的目标为：
约束条件为：
对于Hinge损失：
优化的目标是要求：
在上述的函数
中引入截距γ，即：
并在上述的最优化问题中增加L2正则，即变成：
至此，令下面的不等式成立：
约束条件为
则Hinge最小化问题变成：
约束条件为：
这与软间隔的SVM是一致的，说明软间隔SVM是在Hinge损失的基础上增加了L2正则。
指数损失是0-1损失函数的一种代理函数，指数损失的具体形式如下：
运用指数损失的典型分类器是AdaBoost算法。
AdaBoost算法是对每一个弱分类器以及每一个样本都分配了权重，对于弱分类器φj的权重为：
其中，
表示的是误分类率。对于每一个样本的权重为：
最终通过对所有分类器加权得到最终的输出。
对于指数损失函数：
可以得到需要优化的损失函数：
假设f~表示已经学习好的函数，则有：
而：
通过最小化φ，可以得到：
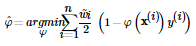
将其代入上式，进而对θ求最优解，得：
其中，
可以发现，其与AdaBoost是等价的。
5、感知损失
5.1、感知损失
感知损失是Hinge损失的一个变种，感知损失的具体形式如下：
运用感知损失的典型分类器是感知机算法。
感知机算法只需要对每个样本判断其是否分类正确，只记录分类错误的样本，其损失函数为：
对于感知损失：
优化的目标为：
在上述的函数
中引入截距b，即：
上述的形式转变为：
对于max函数中的内容，可知：
对于错误的样本，有：
类似于Hinge损失，令下式成立：
约束条件为：
则感知损失变成：
即为：
Hinge损失对于判定边界附近的点的惩罚力度较高，而感知损失只要样本的类别判定正确即可，而不需要其离判定边界的距离，这样的变化使得其比Hinge损失简单，但是泛化能力没有Hinge损失强。数据分析师培训
import matplotlib.pyplot as plt
import numpy as np
xmin, xmax = -4, 4
xx = np.linspace(xmin, xmax, 100)
plt.plot([xmin, 0, 0, xmax], [1, 1, 0, 0], 'k-', label="Zero-one loss")
plt.plot(xx, np.where(xx < 1, 1 - xx, 0), 'g-', label="Hinge loss")
plt.plot(xx, np.log2(1 + np.exp(-xx)), 'r-', label="Log loss")
plt.plot(xx, np.exp(-xx), 'c-', label="Exponential loss")
plt.plot(xx, -np.minimum(xx, 0), 'm-', label="Perceptron loss")
plt.ylim((0, 8))
plt.legend(loc="upper right")
plt.xlabel(r"Decision function $f(x)$")
plt.ylabel("$L(y, f(x))$")
plt.show()
数据分析咨询请扫描二维码
