 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
上一篇介绍了关联规则挖掘的一些基本概念和经典的Apriori算法,Aprori算法利用频繁集的两个特性,过滤了很多无关的集合,效率提高不少,但是我们发现Apriori算法是一个候选消除算法,每一次消除都需要扫描一次所有数据记录,造成整个算法在面临大数据集时显得无能为力。今天我们介绍一个新的算法挖掘频繁项集,效率比Aprori算法高很多。
FpGrowth算法通过构造一个树结构来压缩数据记录,使得挖掘频繁项集只需要扫描两次数据记录,而且该算法不需要生成候选集合,所以效率会比较高。我们还是以上一篇中用的数据集为例:
| TID | Items |
| T1 | {牛奶,面包} |
| T2 | {面包,尿布,啤酒,鸡蛋} |
| T3 | {牛奶,尿布,啤酒,可乐} |
| T4 | {面包,牛奶,尿布,啤酒} |
| T5 |
{面包,牛奶,尿布,可乐} |
一、构造FpTree
FpTree是一种树结构,树结构定义如下:

树的每一个结点代表一个项,这里我们先不着急看树的结构,我们演示一下FpTree的构造过程,FpTree构造好后自然明白了树的结构。假设我们的最小绝对支持度是3。
Step 1:扫描数据记录,生成一级频繁项集,并按出现次数由多到少排序,如下所示:
| Item | Count |
| 牛奶 | 4 |
| 面包 | 4 |
| 尿布 | 4 |
| 啤酒 | 3 |
可以看到,鸡蛋和可乐没有出现在上表中,因为可乐只出现2次,鸡蛋只出现1次,小于最小支持度,因此不是频繁项集,根据Apriori定理,非频繁项集的超集一定不是频繁项集,所以可乐和鸡蛋不需要再考虑。
Step 2:再次扫描数据记录,对每条记录中出现在Step 1产生的表中的项,按表中的顺序排序。初始时,新建一个根结点,标记为null;
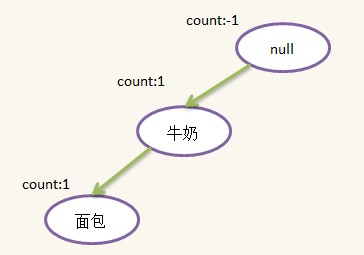
1)第一条记录:{牛奶,面包},按Step 1表过滤排序得到依然为{牛奶,面包},新建一个结点,idName为{牛奶},将其插入到根节点下,并设置count为1,然后新建一个{面包}结点,插入到{牛奶}结点下面,插入后如下所示:
2)第二条记录:{面包,尿布,啤酒,鸡蛋},过滤并排序后为:{面包,尿布,啤酒},发现根结点没有包含{面包}的儿子(有一个{面包}孙子但不是儿子),因此新建一个{面包}结点,插在根结点下面,这样根结点就有了两个孩子,随后新建{尿布}结点插在{面包}结点下面,新建{啤酒}结点插在{尿布}下面,插入后如下所示:

3)第三条记录:{牛奶,尿布,啤酒,可乐},过滤并排序后为:{牛奶,尿布,啤酒},这时候发现根结点有儿子{牛奶},因此不需要新建结点,只需将原来的{牛奶}结点的count加1即可,往下发现{牛奶}结点有一个儿子{尿布},于是新建{尿布}结点,并插入到{牛奶}结点下面,随后新建{啤酒}结点插入到{尿布}结点后面。插入后如下图所示:

4)第四条记录:{面包,牛奶,尿布,啤酒},过滤并排序后为:{牛奶,面包,尿布,啤酒},这时候发现根结点有儿子{牛奶},因此不需要新建结点,只需将原来的{牛奶}结点的count加1即可,往下发现{牛奶}结点有一个儿子{面包},于是也不需要新建{面包}结点,只需将原来{面包}结点的count加1,由于这个{面包}结点没有儿子,此时需新建{尿布}结点,插在{面包}结点下面,随后新建{啤酒}结点,插在{尿布}结点下面,插入后如下图所示:

5)第五条记录:{面包,牛奶,尿布,可乐},过滤并排序后为:{牛奶,面包,尿布},检查发现根结点有{牛奶}儿子,{牛奶}结点有{面包}儿子,{面包}结点有{尿布}儿子,本次插入不需要新建结点只需更新count即可,示意图如下:

按照上面的步骤,我们已经基本构造了一棵FpTree(Frequent Pattern Tree),树中每天路径代表一个项集,因为许多项集有公共项,而且出现次数越多的项越可能是公公项,因此按出现次数由多到少的顺序可以节省空间,实现压缩存储,另外我们需要一个表头和对每一个idName相同的结点做一个线索,方便后面使用,线索的构造也是在建树过程形成的,但为了简化FpTree的生成过程,我没有在上面提到,这个在代码有体现的,添加线索和表头的Fptree如下:

至此,整个FpTree就构造好了,在下面的挖掘过程中我们会看到表头和线索的作用。
二、利用FpTree挖掘频繁项集
FpTree建好后,就可以进行频繁项集的挖掘,挖掘算法称为FpGrowth(Frequent Pattern Growth)算法,挖掘从表头header的最后一个项开始。
1)此处即从{啤酒}开始,根据{啤酒}的线索链找到所有{啤酒}结点,然后找出每个{啤酒}结点的分支:{牛奶,面包,尿布,啤酒:1},{牛奶,尿布,啤酒:1},{面包,尿布,啤酒:1},其中的“1”表示出现1次,注意,虽然{牛奶}出现4次,但{牛奶,面包,尿布,啤酒}只同时出现1次,因此分支的count是由后缀结点{啤酒}的count决定的,除去{啤酒},我们得到对应的前缀路径{牛奶,面包,尿布:1},{牛奶,尿布:1},{面包,尿布:1},根据前缀路径我们可以生成一颗条件FpTree,构造方式跟之前一样,此处的数据记录变为:
| TID | Items |
| T1 | {牛奶,面包,尿布} |
| T2 | {牛奶,尿布} |
| T3 | {面包,尿布} |
绝对支持度依然是3,构造得到的FpTree为:
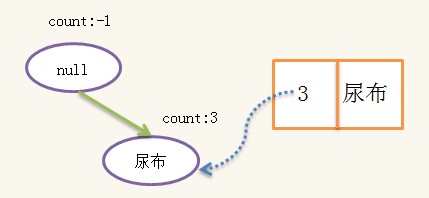
构造好条件树后,对条件树进行递归挖掘,当条件树只有一条路径时,路径的所有组合即为条件频繁集,假设{啤酒}的条件频繁集为{S1,S2,S3},则{啤酒}的频繁集为{S1+{啤酒},S2+{啤酒},S3+{啤酒}},即{啤酒}的频繁集一定有相同的后缀{啤酒},此处的条件频繁集为:{{},{尿布}},于是{啤酒}的频繁集为{{啤酒}{尿布,啤酒}}。
2)接下来找header表头的倒数第二个项{尿布}的频繁集,同上可以得到{尿布}的前缀路径为:{面包:1},{牛奶:1},{牛奶,面包:2},条件FpTree的数据集为:
| TID | Items |
| T1 | {面包} |
| T2 | {牛奶} |
| T3 | {牛奶,面包} |
| T4 | {牛奶,面包} |
注意{牛奶,面包:2},即{牛奶,面包}的count为2,所以在{牛奶,面包}重复了两次,这样做的目的是可以利用之前构造FpTree的算法来构造条件Fptree,不过这样效率会降低,试想如果{牛奶,面包}的count为20000,那么就需要展开成20000条记录,然后进行20000次count更新,而事实上只需要对count更新一次到20000即可。这是实现上的优化细节,实践中当注意。构造的条件FpTree为:
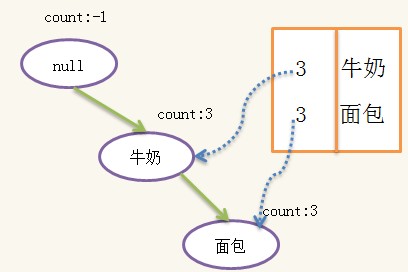
这颗条件树已经是单一路径,路径上的所有组合即为条件频繁集:{{},{牛奶},{面包},{牛奶,面包}},加上{尿布}后,又得到一组频繁项集{{尿布},{牛奶,尿布},{面包,尿布},{牛奶,面包,尿布}},这组频繁项集一定包含一个相同的后缀:{尿布},并且不包含{啤酒},因此这一组频繁项集与上一组不会重复。
重复以上步骤,对header表头的每个项进行挖掘,即可得到整个频繁项集,可以证明(严谨的算法和证明可见参考文献[1]),频繁项集即不重复也不遗漏。
程序的实现代码还是放在我的github上,这里看一下运行结果:

另外我下载了一个购物篮的数据集,数据量较大,测试了一下FpGrowth的效率还是不错的。FpGrowth算法的平均效率远高于Apriori算法,但是它并不能保证高效率,它的效率依赖于数据集,当数据集中的频繁项集的没有公共项时,所有的项集都挂在根结点上,不能实现压缩存储,而且Fptree还需要其他的开销,需要存储空间更大,使用FpGrowth算法前,对数据分析一下,看是否适合用FpGrowth算法。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在数据分析、业务决策、科学研究等领域,统计模型是连接原始数据与业务价值的核心工具——它通过对数据的规律提炼、变量关联分析 ...
2026-02-14在SQL查询实操中,SELECT * 与 SELECT 字段1, 字段2,...(指定个别字段)是最常用的两种查询方式。很多开发者在日常开发中,为了 ...
2026-02-14对CDA(Certified Data Analyst)数据分析师而言,数据分析的核心不是孤立解读单个指标数值,而是构建一套科学、完整、贴合业务 ...
2026-02-14在Power BI实操中,函数是实现数据清洗、建模计算、可视化呈现的核心工具——无论是简单的数据筛选、异常值处理,还是复杂的度量 ...
2026-02-13在互联网运营、产品迭代、用户增长等工作中,“留存率”是衡量产品核心价值、用户粘性的核心指标——而次日留存率,作为留存率体 ...
2026-02-13对CDA(Certified Data Analyst)数据分析师而言,指标是贯穿工作全流程的核心载体,更是连接原始数据与业务洞察的关键桥梁。CDA ...
2026-02-13在机器学习建模实操中,“特征选择”是提升模型性能、简化模型复杂度、解读数据逻辑的核心步骤——而随机森林(Random Forest) ...
2026-02-12在MySQL数据查询实操中,按日期分组统计是高频需求——比如统计每日用户登录量、每日订单量、每日销售额,需要按日期分组展示, ...
2026-02-12对CDA(Certified Data Analyst)数据分析师而言,描述性统计是贯穿实操全流程的核心基础,更是从“原始数据”到“初步洞察”的 ...
2026-02-12备考CDA的小伙伴,专属宠粉福利来啦! 不用拼运气抽奖,不用复杂操作,只要转发CDA真题海报到朋友圈集赞,就能免费抱走实用好礼 ...
2026-02-11在数据科学、机器学习实操中,Anaconda是必备工具——它集成了Python解释器、conda包管理器,能快速搭建独立的虚拟环境,便捷安 ...
2026-02-11在Tableau数据可视化实操中,多表连接是高频操作——无论是将“产品表”与“销量表”连接分析产品销量,还是将“用户表”与“消 ...
2026-02-11在CDA(Certified Data Analyst)数据分析师的实操体系中,统计基本概念是不可或缺的核心根基,更是连接原始数据与业务洞察的关 ...
2026-02-11在数字经济飞速发展的今天,数据已成为核心生产要素,渗透到企业运营、民生服务、科技研发等各个领域。从个人手机里的浏览记录、 ...
2026-02-10在数据分析、实验研究中,我们经常会遇到小样本配对数据的差异检验场景——比如同一组受试者用药前后的指标对比、配对分组的两组 ...
2026-02-10在结构化数据分析领域,透视分析(Pivot Analysis)是CDA(Certified Data Analyst)数据分析师最常用、最高效的核心实操方法之 ...
2026-02-10在SQL数据库实操中,字段类型的合理设置是保证数据运算、统计准确性的基础。日常开发或数据分析时,我们常会遇到这样的问题:数 ...
2026-02-09在日常办公数据分析中,Excel数据透视表是最常用的高效工具之一——它能快速对海量数据进行分类汇总、分组统计,将杂乱无章的数 ...
2026-02-09表结构数据作为结构化数据的核心载体,其“获取-加工-使用”全流程,是CDA(Certified Data Analyst)数据分析师开展专业工作的 ...
2026-02-09在互联网产品运营、用户增长的实战场景中,很多从业者都会陷入一个误区:盲目投入资源做推广、拉新,却忽视了“拉新后的用户激活 ...
2026-02-06