本篇目录
统计学是一门收集、处理、分析、解释数据并从中得出结论的科学。
一、基本符号表
| 符号 | 含义 |
|---|---|
| X | 总体(随机变量,可带分布) |
| Xi | 样本(随机变量,可带分布,可组成统计量) |
| xi | 样本实际观测值(实数) |
| μ | 总体均值 |
| π | 总体比例 |
| σ | 总体标准差 |
| σ2 | 总体方差 |
| X | 样本均值(统计量,可带分布) |
| P | 样本比例(统计量,可带分布) |
| S | 样本标准差(统计量,可带分布) |
| S2 | 样本方差(统计量,可带分布) |
| x | 样本均值(实数,根据样本集计算而来) |
| p | 样本比例(实数,根据样本集计算而来) |
| s | 样本标准差(实数,根据样本集计算而来) |
| s2 | 样本方差 (实数,根据样本集计算而来) |
| Mo | 众数 |
| Me | 中位数 |
| QL | 下四分位数 |
| QU | 上四分位数 |
| x | 算术平均数 |
| H | 调和平均数 |
| G | 集合平均数 |
| R | 极差 |
| Md | 平均差 |
| Vs | 变异系数 |
| Sk | 偏态系数 |
| K | 峰态系数 |
二、数据的分类
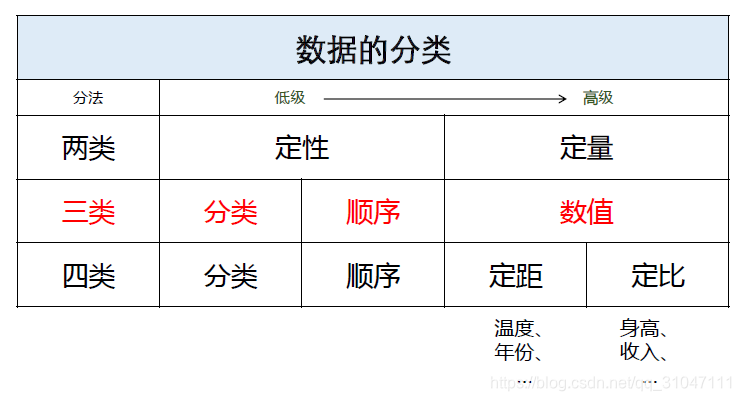
区间(分组的数值型数据)仍属于数值型
不同类型数据之间往往可以进行转换(高级→低级,反之不行)
低级数据的方法高级数据可以用,但高级数据的方法低级数据不可以用
三、统计方法之 描述性分析方法
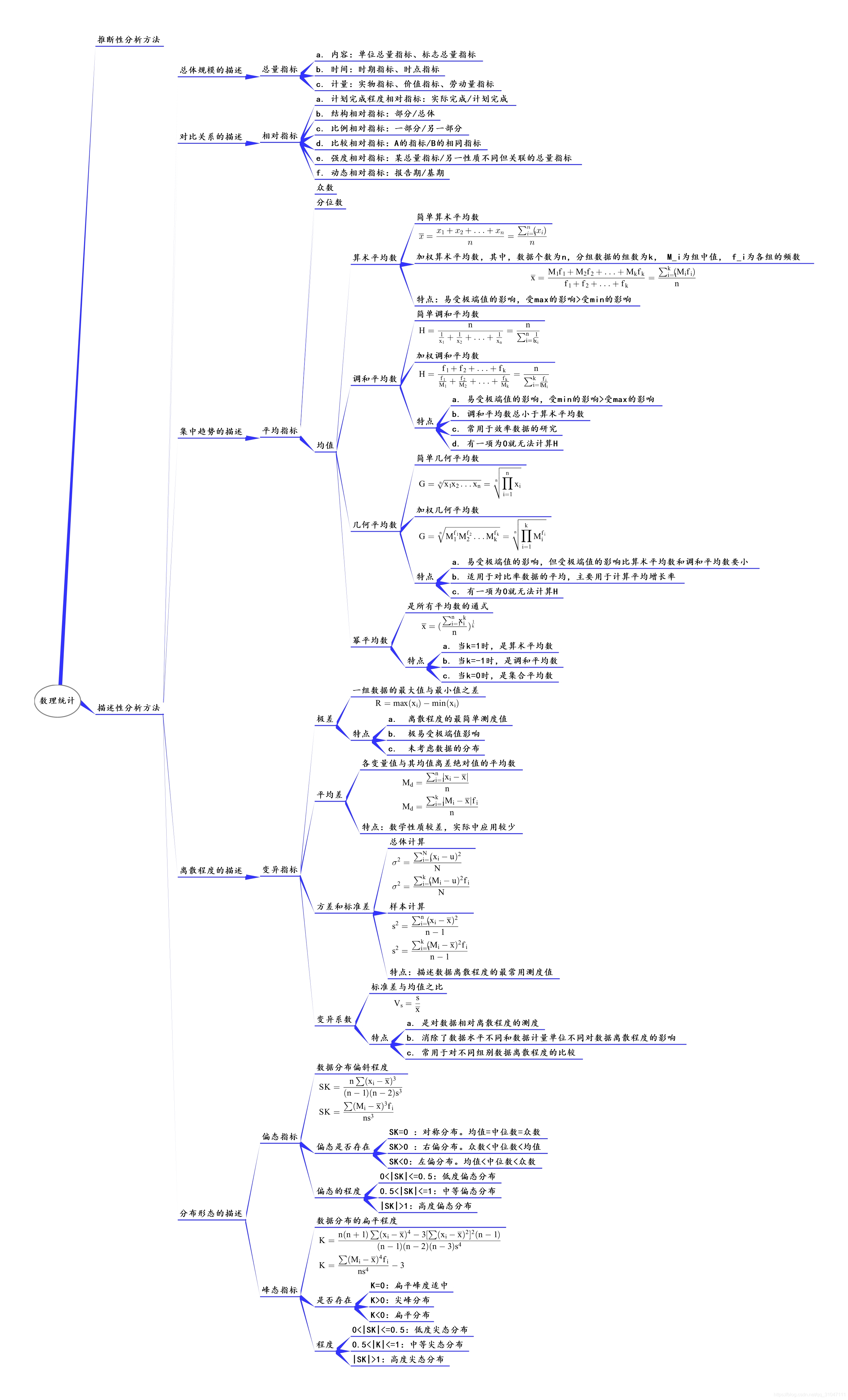
四、统计方法之 推断性分析方法
I、各类分布
1. 0-1分布

2. 二项分布
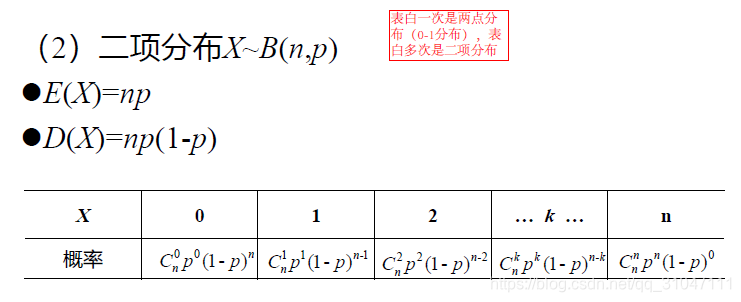
3. 正态分布
4. 标准正态分布
5. 卡方分布
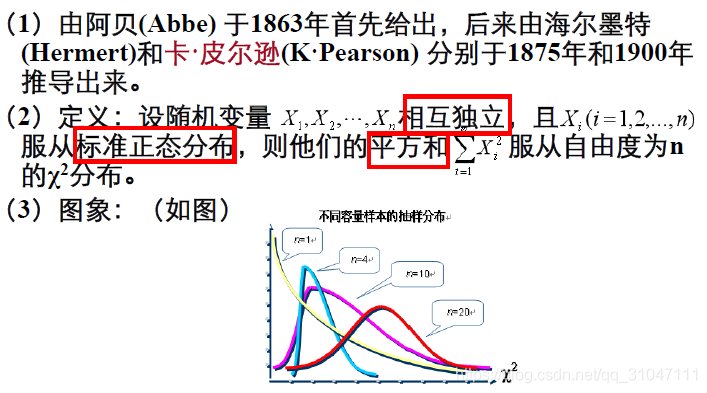
6. t分布
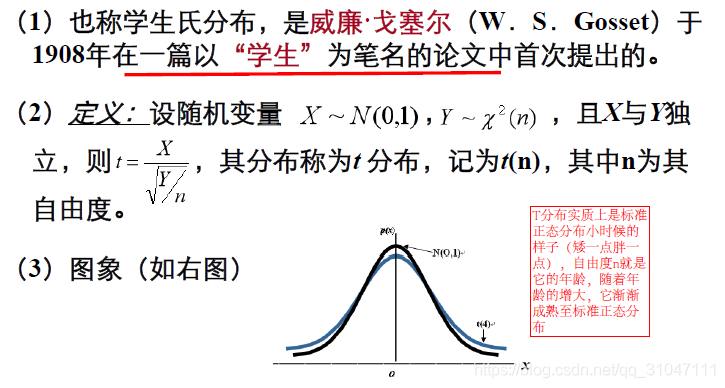
7. F分布
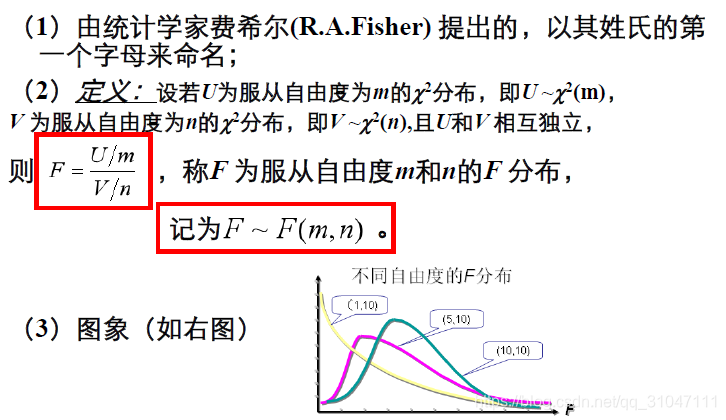
8. 各分布的联系
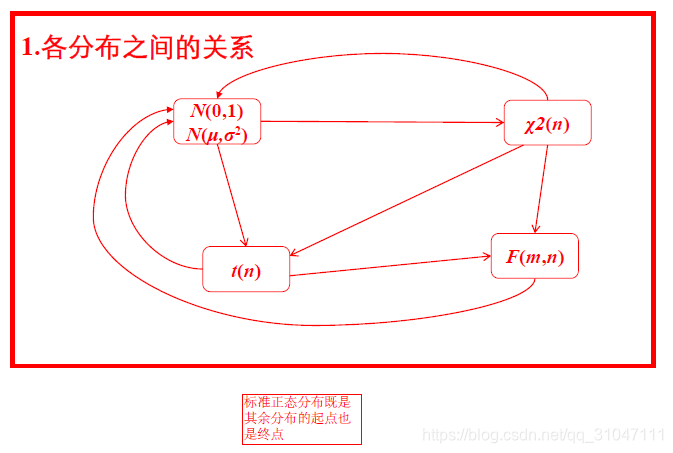
9. 分布函数与分位点的联系

II、估计
1. 选定欲估计的总体参数

2. 选定总体参数对应的样本统计量
其实此处的x,π,s2都应该大写,因为它们代表的是实际样本计算值,而非样本统计量。

3. 确定统计量的抽样分布






4. 利用统计量的分布和实际样本集数据来对总体参数进行点估计或区间估计操作
点估计方法(估计总体参数的具体值):矩估计法、最大似然法和顺序估计量估计法。



区间估计方法(估计总体参数的出现区间):置信水平(1−α)一般取90%、95%和99%。


III、假设检验
1. 选择某总体参数并对其提出假设



2. 根据总体参数确定对应的检验统计量


3. 规定显著性水平值
一般取值为0.01,0.05,0.1
4. 确定检验统计量的抽样分布,并据此计算检验统计量的实际样本值



5. 根据原假设来判断拒绝域的位置,并利用实际样本值是否落在拒绝域(具体值查表即可)进行决策
α临界值法:
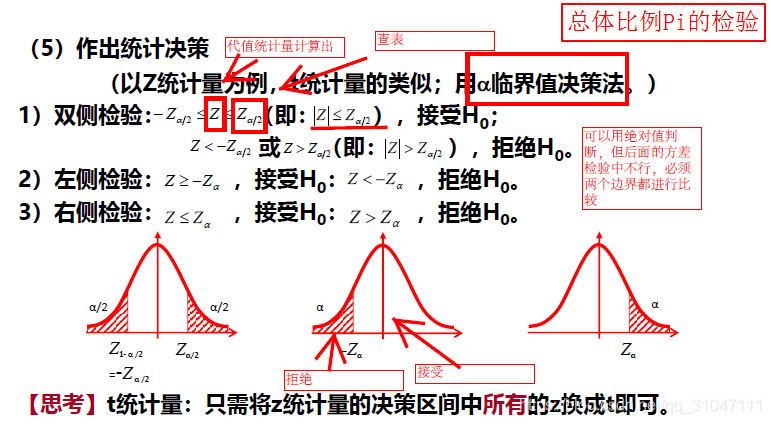
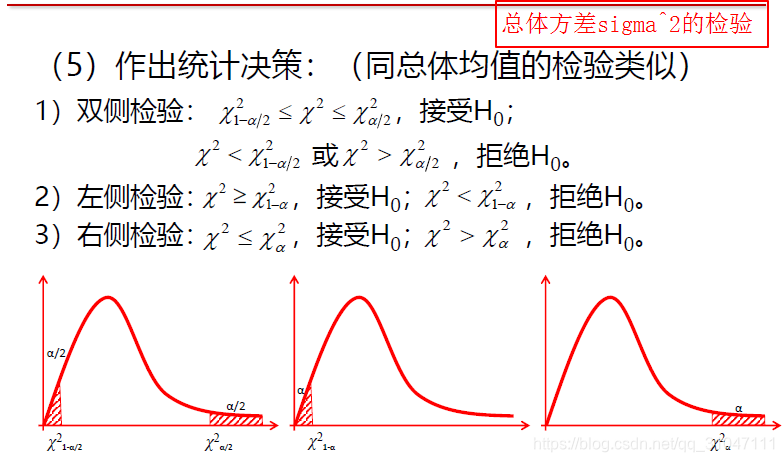
P值法:

置信区间法:无
IV. 列联分析
本质是对每个总体的比例参数是否相等进行假设检验,因此下面的每一步都可以和假设检验步骤进行对应。
1. 提出对总体比例参数的假设(一般为双侧检验)

2. 构造边缘分布表
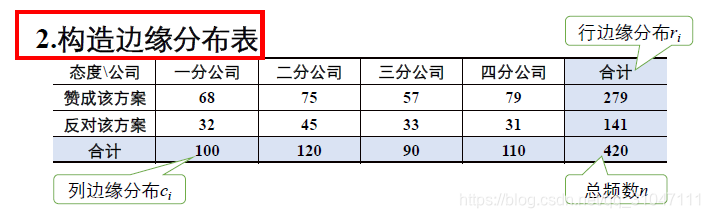
3. 计算期望频数
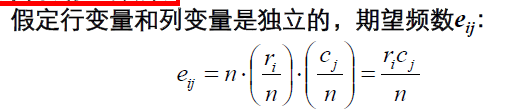
4. 构造总体比例对应的统计量的卡方分布,并计算统计量的实际样本值

5. 根据拒绝域(右侧检验)来得出结论
一般默认显著性水平α为0.05,若χ2<χα2(自由度),则接受原假设,否则拒绝。
7.列联分析步骤五的改进
为了填补由于样本量的不同而影响决策结果的缺陷,因此根据ϕ相关系数来得出结论。其中样本总量n指的是边缘分布表总频数。

8. 列联分析的拓展应用

V. 方差分析
1. 提出对总体均值参数假设(一般为双侧检验)

2. 分析差异

3. 计算均方(SSE和SSA)
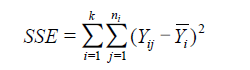
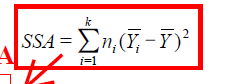
4. 构造总体均值对应的统计量的F分布,并计算样本统计量值F=MSA/MSE
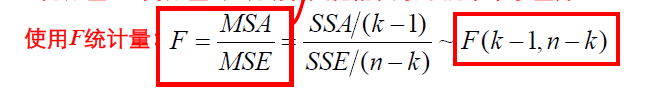
其中,k代表的是组的个数,n代表的是总样本数。
5. 根据规定的显著性水平和F分布的自由度确定拒绝域(右侧检验)查临界值,并决策
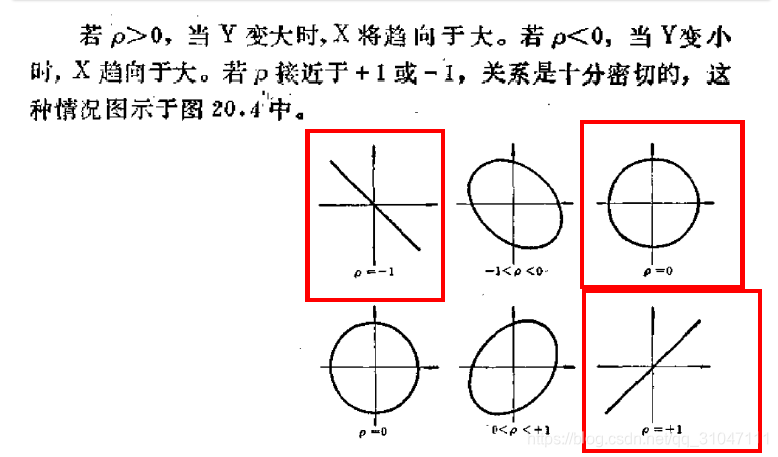
VI. 相关分析
研究的是有没有关系,关系有多大的问题。



VII. 回归分析
研究的是关系是什么,因此在做对关系进行分析的研究中,需要先使用相关分析判断有没有关系,再考虑使用回归分析。












 0
0




 发表评论
发表评论







