距离度量——闵可夫斯基距离的定义与公式_CDA答疑社区

热线电话：13121318867

登录

dreamhappy2012

2019-01-24 阅读量: 2490

距离度量——闵可夫斯基距离的定义与公式

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

闵氏距离定义：
两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

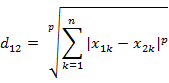
闵式距离n维

其中p是一个变参数：

当p=1时，就是曼哈顿距离；

当p=2时，就是欧氏距离；

当p→∞时，就是切比雪夫距离。

因此，根据变参数的不同，闵氏距离可以表示某一类/种的距离。

闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
e.g. 二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。那么a与b的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。
闵氏距离的缺点：
(1)将各个分量的量纲(scale)，也就是“单位”相同的看待了;
(2)未考虑各个分量的分布（期望，方差等）可能是不同的。

46.1538

1

0

关注作者

收藏

评论(0)

发表评论

暂无数据

CDA考试动态

CDA报考指南

推荐帖子