核岭回归与SVR的比较

啊啊啊啊啊吖

2018-12-06 阅读量: 1636

核岭回归与SVR的比较

核岭回归（KRR）和SVR都通过采用核技巧来学习非线性函数，即，它们学习由相应核引起的空间中的线性函数，其对应于原始空间中的非线性函数。它们的损失函数不同（脊与ε不敏感损失）。与SVR相比，拟合KRR可以以封闭形式完成，对于中等大小的数据集通常更快。另一方面，学习模型是非稀疏的，因此在预测时比SVR慢。

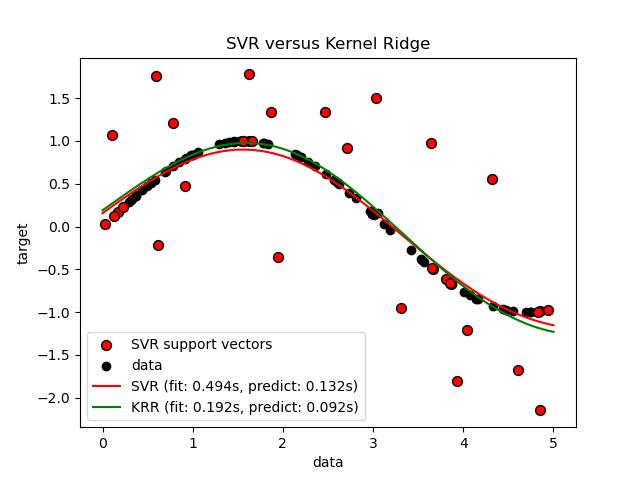
此示例说明了人工数据集上的两种方法，这些方法由正弦目标函数和添加到每第五个数据点的强噪声组成。第一个图比较了当使用网格搜索优化RBF内核的复杂性/正则化和带宽时KRR和SVR的学习模型。学到的功能非常相似; 然而，拟合KRR约为。比拟合SVR快7倍（均采用网格搜索）。然而，使用SVR预测100000个目标值的速度比树速度快了十倍以上，因为它只使用了大约数据来学习稀疏模型。100个训练数据点中的1/3作为支持向量。

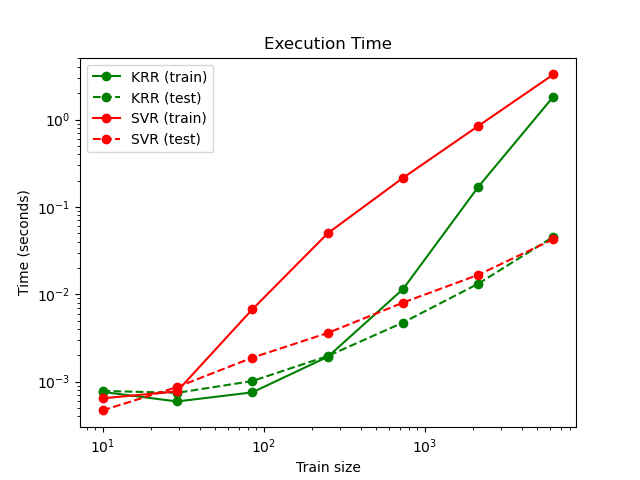
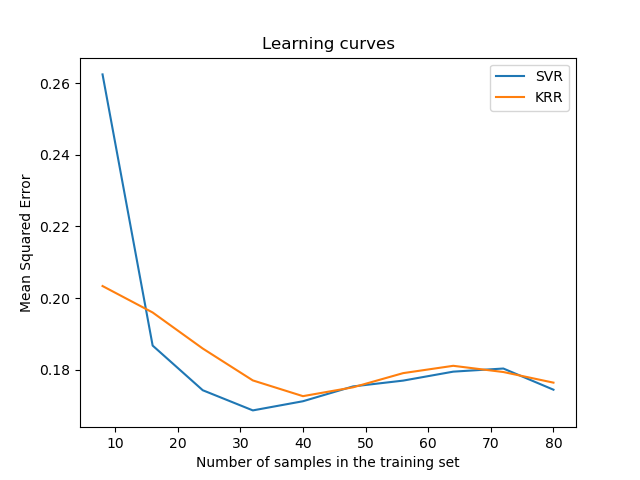
下图比较了不同大小训练集的KRR和SVR的拟合和预测时间。对于中型训练集（小于1000个样本），拟合KRR比SVR快; 然而，对于更大的训练集，SVR更好地扩展。关于预测时间，由于学习的稀疏解，所以训练集的所有大小的SVR都快于KRR。注意，稀疏程度以及预测时间取决于SVR的参数epsilon和C.

../_images/sphx_glr_plot_kernel_ridge_regression_001.png

../_images/sphx_glr_plot_kernel_ridge_regression_002.png

../_images/sphx_glr_plot_kernel_ridge_regression_003.png

0.0000

关注作者

发表评论

暂无数据

CDA考试动态

CDA报考指南

推荐帖子