怎么理解理论上的概率估计？_CDA答疑社区

热线电话：13121318867

登录

詹惠儿

2018-11-30 阅读量: 808

怎么理解理论上的概率估计？

为了更好地理解这两个模型及其所做的假设，让我们回过头来看看我们如何在第11章第12章中推导出他们的分类规则。我们通过将文档分配给类来决定文档的类成员资格概率（参见概率），我们计算如下：

利用这一点，

以这种方式添加是一种简单的平滑形式。对于具有分类结果的试验（例如注意术语的存在或不存在），从数据估计事件概率的一种方法是简单地计算事件发生的次数除以试验总数。这被称为事件的相对频率。估计相对频率为的概率最大似然估计（或MLE），因为该值使观察到的数据最大可能。然而，如果我们简单地使用MLE，那么我们碰巧看到的事件的概率通常太高，而其他事件可能是完全看不到的并且给它们作为概率估计它们的相对频率0都是低估的，并且通常打破我们的模型，因为任何乘以0都是0.同时降低所见事件的估计概率并增加看不见事件的概率被称为平滑。一种简单的平滑方法是

为每个观察到的计数添加一个数字。这些伪计量对应于在词汇表中使用均匀分布作为贝叶斯先前，按照公式 59。我们最初假设事件的均匀分布，其中大小

$$ \ $阿尔法$

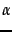
表示我们对均匀性的信念强度，然后我们根据观察到的事件更新概率。由于我们对均匀性的信念很弱，我们使用。这是一种形式

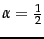
$\ alpha = \ frac {1} {2}$

最大后验（MAP）估计，其中我们根据等式59，基于先验和观察到的证据选择概率的最可能点值。以给出概率模型 ;简单的方法添加

$\压裂{1} {2}$

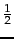
到每个观察到的计数现在将做。

0.0000

0

2

关注作者

收藏

评论(0)

发表评论

暂无数据

CDA考试动态

CDA报考指南

推荐帖子