离群值的判断与处理

我们在数据分析的时候，经常会碰到某些数据远远大于或小于其他数据，这些明显偏离的数据就是离群值，也叫奇异值、极端值。

离群值产生的原因大致有两点：

1.总体固有变异的极端表现，这是真实而正常的数据，只是在这次实验中表现的有些极端，这类离群值与其余观测值属于同一总体。

2.由于试验条件和实验方法的偶然性，或观测、记录、计算时的失误所产生的结果，是一种非正常的、错误的数据，这些数据与其余观测值不属于同一总体。

由于数据的分布不同，判断离群值的方法也有所差别，在此只介绍国标GB/T4883-2008对于正态分布情况下的离群值判断方法，其他分布情况下，我还没有找到相关资料。

对于离群值，国标也有一些概念定义：

1.检出水平
为检验出离群值而指定的统计检验的显著性水平，和大多数检验一样，α一般为0.05

2.剔除水平
为检验出离群值是否为高度离群值而指定的统计检验的显著性水平，剔除水平α*不应超过检出水平α，通常为0.01，个人认为这个剔除水平就是判断该离群值是否需要实际剔除，也就是说该离群值有可能是第二类原因产生的非正常样本数据。

3.统计离群值
在剔除水平下统计检验为显著的离群值

4.歧离值
在检出水平下显著，而在剔除水平下不显著的离群值。
================================================

正态分布情况下的离群值判断方法，大致可分为两类：可以检验剔除水平和不可检验剔除水平

一、可检验剔除水平

1.总体标准差已知时，奈尔检验法

对样本数据按从小到大顺序排序，
如怀疑最大值X_(n)为最大值，则计算统计量R_n

确定检出水平α，查奈尔系数表（见国标GB/T4883-2008），得出临界值

当R_n>R_1-α(n)时，判定X_(n)为离群值，否则不能判定

确定剔除水平α*，查奈尔系数表（见国标GB/T4883-2008），得出临界值

当R_n>R_1-α*(n)时，判定X_(n)为统计离群值，否则不能判定

如怀疑最小值X₍₁₎为最大值，则计算统计量R_n'

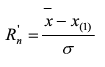
确定检出水平α，查奈尔系数表（见国标GB/T4883-2008），得出临界值
当R_n'>R_1-α(n)时，判定X₍₁₎为离群值，否则不能判定
确定剔除水平α*，查奈尔系数表（见国标GB/T4883-2008），得出临界值
当R_n'>R_1-α*(n)时，判定X₍₁₎为统计离群值，否则不能判定

2.总体标准差未知时，格拉布斯检验法

对样本数据按从小到大顺序排序，然后计算样本均值和样本标准差s


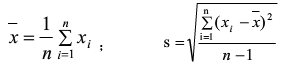
如怀疑最大值X(n)为最大值，计算统计量Gn

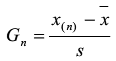
确定检出水平α，查出格拉布斯系数表（见国标GB/T4883-2008），得出临界值
当G_n>G_1-α(n)时，判定X_(n)为离群值，否则不能判定
确定剔除水平α*，查出格拉布斯系数表（见国标GB/T4883-2008），得出临界值
当G_n>G_1-α*(n)时，判定X_(n)为统计离群值，否则不能判定

如怀疑最小值X₍₁₎为最大值，则计算统计量G_n'

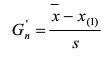
确定检出水平α，查出格拉布斯系数表（见国标GB/T4883-2008），得出临界值
当G_n'>G_1-α(n)时，判定X₍₁₎为离群值，否则不能判定
确定剔除水平α*，查出格拉布斯系数表（见国标GB/T4883-2008），得出临界值
当G_n'>G_1-α*(n)时，判定X₍₁₎为统计离群值，否则不能判定

3.总体标准差未知时，狄克逊(Dixon)检验法

对样本数据按从小到大顺序排序

样本量n在3-30时

计算统计量


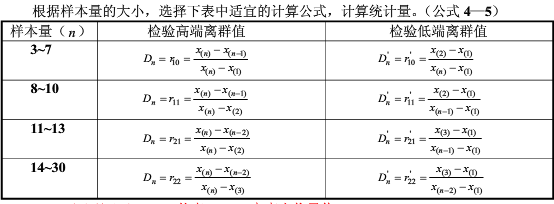
样本量n在30-100时
计算统计量



确定检出水平α，查狄克逊系数表（见国标GB/T4883-2008），得出临界值
当D_n>D_1-α(n)时，判定高端值X_(n)为离群值，否则不能判定
当D_n'>D_1-α*(n)时，判定低端值X₍₁₎为离群值，否则不能判定

4.总体标准差未知时，偏度-峰度检验法

我们知道峰度和偏度是判断数据是否为正态分布的指标，而离群值则明显偏离样本主体，因此我们也可以使用偏度-峰度检验法来判断离群值

单侧情形——偏度检验法

当离群值处于高端或低端一侧时，可使用偏度检验法判断，首先构造偏度统计量bs

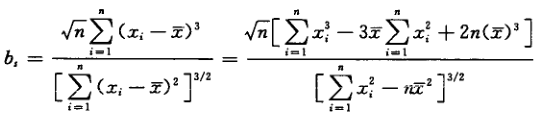
确定检出水平α，查偏度检验系数表（见国标GB/T4883-2008），得出临界值
当b_s>b_1-α(n)时，判定高端值X_(n)为离群值，否则不能判定
当b_s'>b_1-α(n)时，判定低端值X₍₁₎为离群值，否则不能判定

确定剔除水平α*，查偏度系数表（见国标GB/T4883-2008），得出临界值
当b_s>b_1-α*(n)时，判定高端值X_(n)为统计离群值，否则不能判定
当b_s'>b_1-α*(n)时，判定低端值X₍₁₎为统计离群值，否则不能判定

双侧情形——峰度检验法

当高端、低端两侧都可能出现离群值时，可使用峰度检验法判断，首先构造峰度统计量bk

确定检出水平α，查峰度检验系数表（见国标GB/T4883-2008），得出临界值
当b_k>b'_1-α(n)时，判定离均值最远的观测值为离群值，否则判定未发现离群值

确定剔除水平α*，查峰度系数表（见国标GB/T4883-2008），得出临界值
当b_k>b'_1-α*(n)时，判定离均值最远的观测值为统计离群值，否则未发现统计离群值。

二、不可检验剔除水平

1.观察法

根据直方图或四分位图进行判断，现在很多统计软件在绘制这两种图时，都会将离群值特殊标记，一般认为在均值±3倍标准差以外都属于离群值，高出四分位距两倍以上也属于离群值。

2.莱伊达法

又称为3σ准则，在已知总体标准差的情况下使用σ进行判断，但是实际上总体标准差往往未知，因此常使用样本标准差s替代σ，以样本均值替代真值，具体为

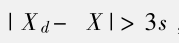
X_d是疑似离群值，X为均值

如果疑似离群值与均值的差值大于三倍标准差，则可认为该值为离群值。

3.肖维特法

统计量

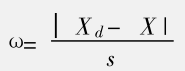
如果计算出的ω值大于肖维特系数表中相应测定次数n时的值，则可认为该值为异常值

3.罗曼诺夫斯基检验法

又称t检验，首先将疑似离群值剔除，然后计算剔除后的均值和标准差

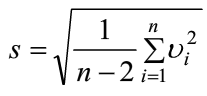
根据测量次数n和显著性水平α，进行t检验，得出系数k，如果

则认为x_^j为离群值

4.4d检验法




5.中位数与算数平均值比较判断法

我们知道中位数居于一组数据中间的数，而均值则可认为是一组数字的“重心”或“平衡点”，当二者相等的时候，可认为这组数字是绝对平衡、没有离群值的，我们可以据此进行判断，当二者相差较大时，表面该组数据可能存在离群值，将疑似离群值剔除之后，再计算均值和中位数，如果二者相差变小，则可认为被剔除值是离群值。

======================================

数据分析师们：判断离群值方法的选择与应注意的问题

1.合理选择离群值的判断方法

离群值的判断方法很多，实际中到底选用哪一个，需根据对测量要求的精准度和测量次数多少来综合确定，一般情况下，测量次数多于30，或大于10次且只做粗略判断时，使用莱伊达法即可；判断精度要求不高，但要求快捷方便时，可以选用4d和中位数与算数平均数比较法。实际上，对于不用查表的方法大都比较便捷，但是代价是精度不够，且无法检验剔除水平，相反一些需要借助查表的方法精度较高但是计算复杂，各有利弊。

2.准确找出离群值

一般情况下，测量列中残差较大者就是疑似离群值，它也就是样本数据中的最大值或最小值
3.查找产生离群值的原因

已经判断为离群值的，即使是统计离群值，也不要简单剔除了之，应进一步分析产生离群值的原因。

推荐学习书籍
《CDA一级教材》适合CDA一级考生备考，也适合业务及数据分析岗位的从业者提升自我。完整电子版已上线CDA网校，累计已有10万+在读~

免费加入阅读：https://edu.cda.cn/goods/show/3151?targetId=5147&preview=0