条件概率是朴素贝叶斯模型的基础。

假设，你的xx公司正在面临着用户流失的压力。虽然，你能计算用户整体流失的概率（流失用户数/用户总数）。但这个数字并没有多大意义，因为资源是有限的，利用这个数字你只能撒胡椒面似的把钱撒在所有用户上，显然不经济。你非常想根据用户的某种行为，精确地估计一个用户流失的概率，若这个概率超过某个阀值，再触发用户挽留机制。这样能把钱花到最需要花的地方。

你搜遍脑子里的数据分析方法，终于，一个250年前的人名在脑中闪现。就是“贝叶斯Bayes”。你取得了近一个月的流失用户数、流失用户中未读消息大于5条的人数、近一个月的活跃用户数及活跃用户中未读消息大于5条的人数。在此基础上，你获得了一个“一旦用户未读消息大于5条，他流失的概率高达%”的精确结论。怎么实现这个计算呢？先别着急，为了解释清楚贝叶斯模型，我们先定义一些名词。

• 概率（Probability）——0和1之间的一个数字，表示一个特定结果发生的可能性。比如投资硬币，“正面朝上”这个特定结果发生的可能性为0.5，这个0.5就是概率。换一种说法，计算样本数据中出现该结果次数的百分比。即你投一百次硬币，正面朝上的次数基本上是50次。
• 几率（Odds）——某一特定结果发生与不发生的概率比。如果你明天电梯上遇上你暗恋的女孩的概率是0.1，那么遇不上她的概率就是0.9，那么遇上暗恋女孩的几率就是1/9，几率的取值范围是0到无穷大。
• 似然（Likelihood）——两个相关的条件概率之比，即给定B发生的情况下，某一特定结果A发生的概率和给定B不发生的情况下A发生的概率之比。另一种表达方式是，给定B的情况下A发生的几率和A的整体几率之比。两个计算方式是等价的。

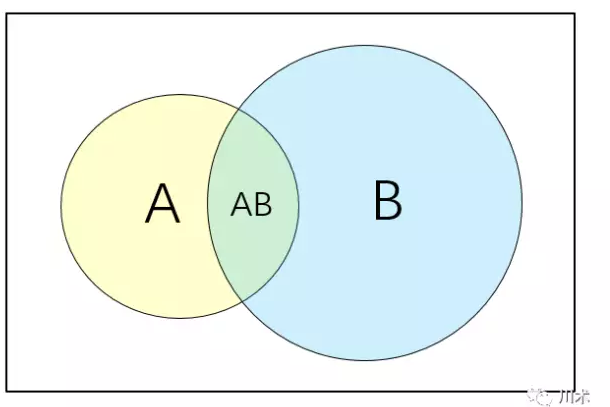
因为上面在似然当中提到了条件概率，那么我们有必要将什么是条件概率做更详尽的阐述。

如上面的韦恩图，我们用矩形表示一个样本空间，代表随机事件发生的一切可能结果。的在统计学中，我们用符号P表示概率，A事件发生的概率表示为P(A)。两个事件间的概率表达实际上相当繁琐，我们只介绍本书中用得着的关系：

1. A事件与B事件同时发生的概率表示为P(A∩B)，或简写为P(AB)即两个圆圈重叠的部分。
2. A不发生的概率为1-P(A)，写为P(~A)，即矩形中除了圆圈A以外的其他部分。
3. A或者B至少有一个发生的概率表示为P(A∪B)，即圆圈A与圆圈B共同覆盖的区域。
4. 在B事件发生的基础上发生A的概率表示为P(A|B)，这便是我们前文所提到的条件概率，图形上它有AB重合的面积比上B的面积。

回到我们的例子。以P(A)代表用户流失的概率，P(B)代表用户有5条以上未读信息的概率，P(B|A)代表用户流失的前提下未读信息大于5条的概率。我们要求未读信息大于5条的用户流失的概率，即P(A|B)，贝叶斯公式告诉我们：

P(A|B)=P(AB)/P(B)

          　　　　=P(B|A)*P(A)/P(B)

从公式中可知，如果要计算B条件下A发生的概率，只需要计算出后面等式的三个部分，B事件的概率（P(B)），是B的先验概率、A属于某类的概率（P(A)），是A的先验概率、以及已知A的某个分类下，事件B的概率（P(B|A)），是后验概率。

如果要确定某个样本归属于哪一类，则需要计算出归属不同类的概率，再从中挑选出最大的概率

我们把上面的贝叶斯公式写出这样，也许你能更好的理解：

MAX(P(Ai|B))=MAX(P(B|Ai)*P(Ai)/P(B))

而这个公式告诉我们，需要计算最大的后验概率，只需要计算出分子的最大值即可，而不同水平的概率P(C)非常容易获得，故难点就在于P(X|C)的概率计算。而问题的解决，正是聪明之处，即贝叶斯假设变量X间是条件独立的，故而P(X|C)的概率就可以计算为：

P(B|Ai) =P(B1/Ai)*P(B2/Ai)*P(B3/Ai)*…..*P(Bn/Ai)

如下图，由这个公式我们就能轻松计算出，在观察到某用户的未读信息大于5条时，他流失的概率为80%。80%的数值比原来的30%真是靠谱太多了。

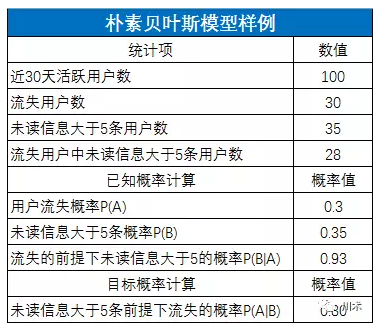
当然，现实情况并不会像这个例子这么理想化。大家会问，凭什么你就会想到用“未读消息大于5条”来作为条件概率？我只能说，现实情况中，你可能要找上一堆觉得能够凸显用户流失的行为，然后一一做贝叶斯规则，来测算他们是否能显著识别用户流失。寻找这个字段的效率，取决于你对业务的理解程度和直觉的敏锐性。另外，你还需要定义“流失”和“活跃”，还需要定义贝叶斯规则计算的基础样本，这决定了结果的精度。

• 利用全概率公式的一个例子

朴素贝叶斯的应用不止于此，我们再例举一个更复杂，但现实场景也更实际的案例。假设你为了肃清电商平台上的恶性商户（刷单、非法交易、恶性竞争等），委托算法团队开发了一个识别商家是否是恶性商户的模型M1。为什么要开发模型呢？因为之前识别恶性商家，你只能通过用户举报和人肉识别异常数据的方式，人力成本高且速率很慢。你指望有智能的算法来提高效率。

之前监察团队的成果告诉我们，目前平台上的恶性商户比率为0.2%，记为P(E)，那么P(~E)就是99.8%。利用模型M1进行检测，你发现在监察团队已判定的恶性商户中，由模型M1所判定为阳性（恶性商户）的人数占比为90%，这是一个条件概率，表示为P(P|E)=90%；在监察团队判定为健康商户群体中，由模型M1判定为阳性的人数占比为8%，表示为P(P|~E)=8%。乍看之下，你是不是觉得这个模型的准确度不够呢？感觉对商户有8%的误杀，还有10%的漏判。其实不然，这个模型的结果不是你想当然的这么使用的

这里，我们需要使用一个称为“全概率公式”的计算模型，来计算出在M1判别某个商户为恶性商户时，这个结果的可信度有多高。这正是贝叶斯模型的核心。当M1判别某个商户为恶性商户时，这个商户的确是恶性商户的概率由P(E|P)表示：

P(E|P)

=P(P|E)*P(E) / (P(E)*P(P|E)+P(~E)*P(P|~E))

上面就是全概率公式。要知道判别为恶性商户的前提下，该商户实际为恶性商户的概率，需要由先前的恶性商户比率P(E)，以判别的恶性商户中的结果为阳性的商户比率P(P|E)，以判别为健康商户中的结果为阳性的比率P(P|~E)，以判别商户中健康商户的比率P(~E)来共同决定。

P(E)     0.2%
P(P|E)  90%
P(~E)   99.8%
P(P|~E)  8%
P(E|P)= P(P|E)*P(E) / (P(E)*P(P|E)+P(~E)*P(P|~E))  2.2%

由上面的数字，带入全概率公式后，我们获得的结果为2.2%。也就是说，根据M1的判别为阳性的结果，某个商户实际为恶性商户的概率为2.2%，是不进行判别的0.2%的11倍。

你可能认为2.2%的概率并不算高。但实际情况下你应该这么思考：被M1模型判别为恶性商户，说明这家商户做出恶性行为的概率是一般商户的11倍，那么，就非常有必要用进一步的手段进行检查了。

恶性商户判别模型真正的使用逻辑应该是如下图所示。我们先用M1进行一轮判别，结果是阳性的商户，说明出现恶性行为的概率是一般商户的11倍，那么有必要用精度更高的方式进行判别，或者人工介入进行检查。精度更高的检查和人工介入，成本都是非常高的。因此M1模型的使用能够使我们的成本得到大幅节约。

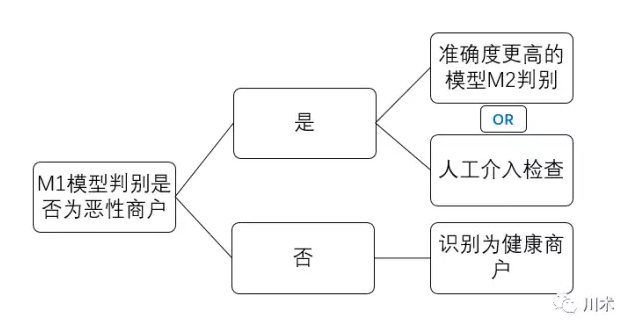
贝叶斯模型在很多方面都有应用，我们熟知的领域就有垃圾邮件识别、文本的模糊匹配、欺诈判别、商品推荐等等。通过贝叶斯模型的阐述，大家应该有这样的一种体会：分析模型并不取决于多么复杂的数学公式，多么高级的软件工具，多么高深的算法组合；它们的原理往往是通俗易懂的，实现起来也没有多高的门槛。比如贝叶斯模型，用Excel的单元格和加减乘除的符号就能实现。所以，不要觉得数据分析建模有多遥远，其实就在你手边。